《圖一　VLSI 解析度及lithography波長的關係(courtesy from Intel)》

若IC製造的誤差的分佈特性已由經驗獲得或能預期，尤其是相關性的資訊，則SSTA就能精巧的利用此一知識去分析製程誤差所造成的良率分佈，線路設計師可用此資訊去預估多晶片生產後的時序分佈，並由此為依據去調整線路設計，以獲得更佳的時序良率。本文章之重點即在於從製程誤差的種類、製程資料的統計分析、及統計型時序分析，有系統的簡介製程?差的分類及分析。

製程誤差之分類

一般而言，製程?差可分為系統性(systematic)及隨機性(random)兩類；系統性的製程?差是指大部份的?差原因應已有詳盡的了解，並可用適當的演算法去預測，例如化學機械研磨(chemical mechanical polishing)後的導線層厚度，經常可以用經驗及數理精確的預估，實因研磨之方式，為一種利用類似大圓盤之壓力及化學藥劑的研磨，由於研磨後之厚度與金屬之密度有相當密切之關聯，因此一般而言，在徹底了解此一機制之後，我們可用化學研磨機的壓力、速度、時間長度、及金屬密度為變數去預估區域厚度。另一個例子，如在光學Lithography時，歷經多年的經驗，IC製造廠其實己經對許多光學特性己有相當的了解，而光學Lithography的模擬也在近年來有長足的發展，雖IC的製造精密度已達小於曝光的波長，因此許多繞許現象無法避免，但長久以來由於OPC(Optical Proximity Correction)的高度發展，許多現象已有長足的了解，因此在製造前即可用光學模擬的方式去預估結果，但許多新的效應，如Dose及Focus的誤差，又須更進一步分析，才能真正了解Lithography的實際誤差來源。

《圖二　 VLSI Doping Density的製程?差造成的電流?移》

《圖三　 CMP之後的層厚度變化》 - BigPic:571x294

《圖四　 lithography的optical proximity effect》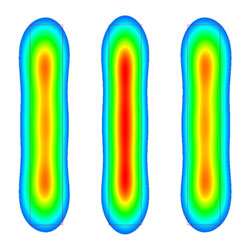

除系統性的製程?差外，當然還有許多製程?差是相當難預估且隨機分佈，因此此類的製程?差為隨機性製程?差，例如，CMOS的Substrate Doping Density經常是隨機分佈且難以精確的控制，造成電晶體的Vt的誤差，因此ITRS (International Technology Roadmap of Semiconductors)估計在不久的未來，Vt的誤差將在IC的效率的最大變因之一。其重要原因是因為Vt其實是Gate oxidation 溫度，n-halo implant dose，gate的長度與 p-halo implant dosage的函數，而這些因素在製造過程中都相當難以控制的。

環境誤差

許多時候，其實對IC效率有影響的不只是製程方面，其實許多在IC運作的外在環境上也有許多其它的變數，例如電力供電的?定度會因IC電流的耗電流量的變化而變化，而如果電流的消耗若可預期，則許多電力振盪可預先計算，則可將此環境誤差轉為系統性。另外一個相當重要的環境變因就是溫度，因IC運作會產生大量的熱，不足的散熱會造成晶體及導線的效率整體變差，而不均勻的散熱更會造熱點(hot spot)，而熱點會造成不均勻的延遲造成運作失敗。在最壞的狀況下，晶片甚至整個電路板都有可能將燒毀，最近我們又看到PS3的過熱現象及XBOX 360的召回導致Microsoft 損失1 billion美元以上，可見散熱問題不可掉以輕心。

《圖五　 本組分析一微處理機的溫度分佈圖》

基本時序分析入門

基本靜態時序分析的目的在算出VLSI數位線路的延遲，尤其是關鍵路徑的時序，關鍵路徑一般為延遲較大的路徑，尤其是那些已超出限制的路徑(slack 為負的)，這種錯誤稱為Setup Time Failure，因其訊號到達時已超過clock的Setup Time requirement。許多時侯，短的路徑也會產生問題，因為在clock在關閉之前此訊號提早改變了flip-flop的值，造成運算錯誤，此種錯誤稱為hold time failure。

一般而言，時序分析可分為兩種，一種為路徑(path-based)為主，一種為區塊(block-based)為主，本文將介紹一個相當簡化的說明：

第一、path-based的分析主要是以路徑為主，從起始點的到達時間一步步的加上各個gate的延遲，例如下圖(a)的線路，路徑i-1-2-o的延遲是，而在o點的信號到達時間(ao)為ai+ d1+d2。

《圖六　 path-based的路徑分析》

第二、block-based的分析主要是以級為主，從所有的輸入開始，它逐步分析?一個gate輸出信號到達時間，例如在圖(a)中的gate 1的輸出時間為a1 =max(ai+ d1，aj+ d1)。

由上述兩種分析可知，path-based做法只須要加法，而block-based則須要max的動作，雖然path-based的做法較簡單，但因path可能有成千上萬個，因此大部份時序分析還是常常須要用到block-based的分析方式。

信號到達統計分佈

當信號的到達時間是形成一統計分佈，而非一定值時，傳統的統計時序分析必須改變，所有gate延遲為一隨機變數，而變數之間可能有所相關。但是值得慶幸的是，加法及max動作不變。

《圖七　gate延遲是一個隨機分佈而非定值》

首先，當兩個統計分佈相加時，它們的平均值(mean)可相加但其變異數(variance)的算法在不相關時有平方合的關係，但在相關時則必須加上修正項，因為所有的相關性的必須併入考量。我們現在簡介此一算法，給定兩隨機變數 X 和 Y， 且各別的平均值(mean)為 ux，和uy且其變異數為sx2，和sy2，且X與Y的共變異數(covariance)為COV(X，Y)，則X+Y的平均值為ux+uy而其新變異數sx+y2滿足sx+y 2= sx 2+ sx 2+ 2COV(X，Y)。若另有許多隨機變數，則矩陣運算必須應用去解決此一問題，雖較繁雜但還可行。由上述可知，其實加法對統計來說是輕而易舉的，所以path-based的統計時序分析方法難度即可立即運用，那麼關於block-based時序分析所需的max運算呢？有點困難的問題，且一般教科書都?有介紹關於max的統計運算，因此，當SSTA開始發展時幾乎都在處理此一問題。先進的考古學家遍查古藉的結果終於發現在1961年時就有人處理此一問題，而之後多數的SSTA研究都借用此數學家clark所提出的觀念[1]，他利用加權後的平均值加上一修正項去計算max後結果的平均值，並且運用平均值、變異數及共變異數的多項式去算出max後的變異數.但其基本之要求為所有隨機變數都是高斯分佈(Gaussian Distribution).為了計算方便，為此，幾乎所有初期SSTA都假設gate的延遲為高斯分佈。

其實，高斯分佈的基本假設之後受到了高度的質疑，有誰能保證所有參數分佈都可用高斯分佈準確的逼近，更何況即使所有參數都是高斯分佈，之後演申出的參數也不見得是高斯分佈，其原因在於許多運算都不只是線性相加的運算而已，例如，即使gate的vt是高斯，但gate 的延遲也不一定能直接用高斯分佈去逼近。讓人更困擾的是，max運算本身其實常造成不稱的分佈，而這個現象直接被clark的公式所忽略了，久而久之，誤差會逐漸加成而變大，而一般ssta本身並不知曉這一重大缺失。

研究成果

為此，本組在2004年之後發表了一系列的文章來解決此一問題，首先提出了利用計算max的skewness (?態)去偵測誤差，若?態太大，則將會延遲max的計算，等到遇到適合的運算時才施行運算，此方法可有效減少max運算的誤算。接著又提出了用二次高斯多項式當做基本的隨機參數形式，此一新的代表式不但同時保持平均值、變異數甚至連?都能完整保持，此一代表法不只是脫去了過去高斯假設，並且容許了非線性運算。近來，又提出了高階高斯多項式去掌握更多的資訊，預計將能為統計型時序分析帶來更多更精準的演算法。

未來要務 製程資料統計分析

經過數年的努力，己逐漸看到SSTA演算法已趨成熟，但其實還有一重要的問題還未解決，那就是製程資料的準備。俗語說，Garbage-in Garbage-out，SSTA極需要正確的統計分析資料才有機會準確的分析出良率，但是製程資料的取得相當不易，即使取得到一些資料，其代表性及充分性還有許多可質疑的地方。而測量又是另外一個問題，要如何去製造少量測試晶片去了解數以萬計的晶片的特性是一個相當困難的事情，而這件事所須的資源包括財力?物力?智力?甚至權力，並不是一般學校教授?EDA公司或foundry可獨立完成的，甚至獲得資料後如何分析出正確的統計關聯性其實還有相當的困難度。本組目前與聯電（UMC）合作，希望能為此問題提出一些答案。

參考文獻

[1] C. Clark， “The greatest of a finite set of random variables，” Operations Research， vol. 9， pp. 85–91， 1961.

[2]H. Chang and S. S. Sapatnekar， “Statistical Timing Analysis Under Spatial Correlations，” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems， Vol. 24， No. 9， pp. 1467 – 1482， September 2005.

[3] Lizheng Zhang， Weijen Chen， Yuhen Hu， John A. Gubner and Charlie Chungping Chen， " Correlation-Preserved Statistical Timing with Quadratic Form of Gaussian Variables ，" IEEE Transactions on Computer-Aided Design of Integrated Circuits And Systems (TCAD)， 2005.

[4] Lizheng Zhang， Weijen Chen， Yuhen Hu and Charlie Chungping Chen， " Statistical Static Timing Analysis with Conditional Linear MAX/MIN Approximation and Extended Canonical Timing Model，" IEEE Transactions on Computer-Aided Design of Integrated Circuits And Systems (TCAD)， 2005.

[5] S. R. Nassif， “Modeling and analysis of manufacturing variations，” CICC， 2001， pp. 223-228.