在目前許多便攜式裝置中,通常都會包含某種形式的立體聲播放電路,例如MP3或網路收音機等應用,雖然市場上已經有許多專門針對這類電路提供的晶片產品,但事實上,設計人員也可以利用相當普遍的低階元件來有效達成相同的功能,本文將討論這類電路一個相當常見的要求,也就是立體聲音量控制。
傳統上聲音的音量控制大都使用具備對數(log)型式或law特性曲線的電位計,主要原因是使用者耳朵對聲音壓力改變的感知接近對數曲線。
基本上,旋鈕式控制的中點大約會對音訊信號造成20dB的衰減,並在逆時針(Counter Clock Wise;CCW)方向衰減大幅提升,而在順時針(Clock Wise;CW)方向的較大音量控制時較為精密。
雖然這樣的作法基本上沒有什麼問題,但有幾個理由可以說明旋鈕元件並不適合應用在小型便攜式設備上,例如空間限制與可靠度就是兩個明顯的例子,使用上/下按鈕搭配上主控處理器是目前電子產品上常見的音量控制介面,不僅帶來了價格低廉的可用解決方案,還可以避免使用笨重的機械式旋鈕。
立體聲電位計還有一個機械追蹤問題,也就是說,由於機械容忍誤差,在進行音量調整時,左右聲道的相互追蹤能力會受到影響,同時目標轉換函數也必須加以考慮,例如真的需要完全衰減?或者是增益調整控制提供如30dB的調整範圍而沒有完全靜音的位置?
數位式電位計
過去幾年,數位式電位計的發展已經越來越普遍,使用梯型電阻結構搭配FET開關,透過數位控制便可以有效地取代某些應用領域中的機械式電位計,表面上看來,使用一對這類元件看起來是進行立體聲音量控制相當符合邏輯的解決方案,但在此之前必須先解決幾個問題。
目前最普遍的可變電阻形式為線性變化,代表了它們的電阻值以相等的級距變化,但是在音訊音量控制上則需要每步階以dB變化的規則,因此在設計上必須要模擬這個對數特性,這時,設計人員已經不再受到機械式電位計的限制。第二個問題是雖然通常數位式變阻器在設計上每個步階變化都採用相等的電阻值,但製程變動的一個副作用是整體端對端的電阻值對每個元件都可能不同,部分更有高達30%的誤差,這在採用兩個獨立數位變阻器提供二聲音通道間緊密匹配的電路設計時必須要加以考慮,進一步的要求則是變動時必須盡可能避免發生突波,因此必須使用先關後開的觸點安排。
設計
以下為增益調整設計,其中為控制一個衰減範圍,但沒有完全衰減選擇,以及較為傳統的CW/CCW音量控制方式的幾個範例,以下的電路假設電源在2.7V到5V之間,並採用低阻抗的參考電壓(VREF=Vcc/2),輸入信號(IN)則由低阻抗電壓源提供。
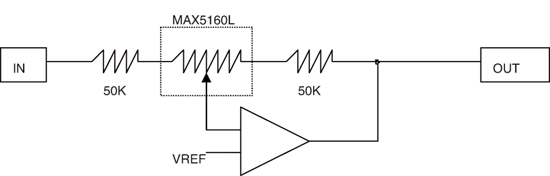
| 《圖一 6dB立體聲增益調整控制、32種增益設定(僅顯示單一通道)。》 |
|
圖一中的電路看起來似乎能夠帶來適當的結果,使用兩個數位輸入控制良好的MAX5160L搭配一個MAX4252,這個電路應該可以提供6dB範圍平衡穩定的追蹤增益或衰減,電路可以在Vcc電源由2.7V到5V的範圍下運作,提供32個可用的增益設定,同時MAX5160L的開機重置狀態還能夠帶來幾近單位植(unity)的增益設定,這個作法的缺點是數位式變阻器整體25%的電阻值變化可能造成通道與通道間以及元件與元件間較大的增益誤差,特別是在電阻值設定在兩個極端阻值時,例如假設50K的電阻誤差為1%,那麼標稱最大+6dB設定可能為:
- Av1= -(50.5K + 62.5K)/49.5K= -2.283 V/V 或 7.16dB
- Av2= -(49.5K + 37.5K)/50.5K= -1.723 V/V 或 4.73dB
左右聲道的不平衡相當容易被發現,這個電路可以透過選擇或調整採用的搭配電阻來解決問題,但這在量產上並不實際,因此必須找出一個能夠將這個增益誤差保持在最低甚至完全加以消除的設計方式。
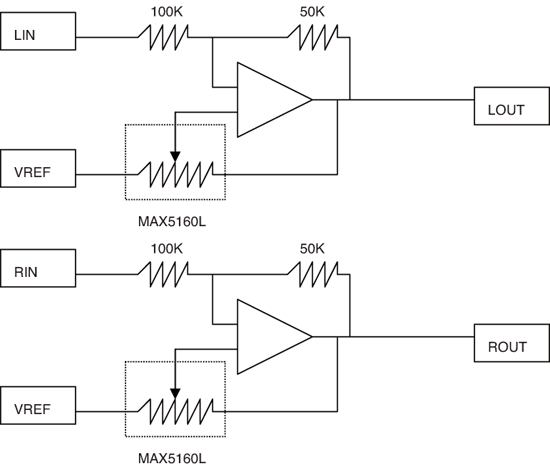
| 《圖二 6dB立體聲增益調整控制、17個增益設定的改善版本。》 |
|
圖二在搭配MAX4252運算放大器的分壓電路中使用了MAX5160L數位式變阻器,並在透過100K與50K電阻組成的常見負回授外加入正回授,這個電路的增益可以表示為:
- AV=(1-Kn)/(Kp-Kn) 其中Kn為負回授分數,Kp為正回授分數。
- (例如在圖二中,Kn = 100K/(100K + 50K)或2/3,Kp為變數)
當MAX5160L的觸點位於VREF端點時,電路的增益為–0.5V/V,因為完全沒有正回授量,當觸點為於中點,也就是Kp=0.5時,這時增益為–2V/V,因此透過使用VREF以及中點間的17個位置變化,增益就可以在6dB的範圍變動,其他的15個未使用位置則為了可重複性而被犧牲,以便讓增益值不像圖一一樣會受到數位式變阻器電阻誤差的影響,因此增益誤差就只受到1%的100K/50K電阻以及MAX5160L的INL/DNL誤差(最高4.6%)的限制。
相當值得注意的一點是,這個電路會在Kp≧23時達到穩定度限制,也就是當正回授分數相等甚至是超過負回授時,因此控制MAX5160L的主控端處理器應該要避免這個情況的發生。
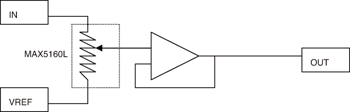
| 《圖三 傳統的音量控制(僅顯示單一通道)具有本身的缺點。》 |
|
圖三的電路顯示了使用數位變阻器形成傳統形式音量控制的簡單方法,所有的設定碼都可使用,設定範圍由0dB到全幅衰減,表一列出了以MAX5160L的32個步階為基礎所計算得出的衰減值。
(表一) 圖三電路的計算結果
控制碼設定 |
衰減值 |
控制碼設定 |
衰減值 |
0 |
0.00 |
16 |
-6.31 |
1 |
-0.28 |
17 |
-6.90 |
2 |
-0.58 |
18 |
-7.55 |
3 |
-0.88 |
19 |
-8.24 |
4 |
-1.20 |
20 |
-9.00 |
5 |
-1.53 |
21 |
-9.83 |
6 |
-1.87 |
22 |
-10.74 |
7 |
-2.22 |
23 |
-11.77 |
8 |
-2.59 |
24 |
-12.93 |
9 |
-2.98 |
25 |
-14.26 |
10 |
-3.38 |
26 |
-15.85 |
11 |
-3.81 |
27 |
-17.79 |
12 |
-4.25 |
28 |
-20.28 |
13 |
-4.72 |
29 |
-23.81 |
14 |
-5.22 |
30 |
-29.83 |
15 |
-5.74 |
31 |
全幅衰減 |
請注意衰減特性的分布情況,在前面15個設定碼中整體變化低於6dB,其中前4個低於1dB,因此沒有什麼特別用處,有趣的是,就算選擇具有更多步階數的元件,依然只能在一半的設定碼中得到6dB的變化。
有時候設計人員會採用的一個作法,是選擇部分可用的設定碼來取得合理穩定的每步階dB變化特性,例如僅使用表一中特別標示的設定碼得到約每步階3dB的變化,總共有11種不同設定值,如果選用的數位變阻器擁有許多接點位置,例如256個或更多時可以有更好的表現,但是這類元件通常較為昂貴,同時由於大部分的接點位置並不會被使用,因此採用不同拓樸結構來嘗試利用更多現有接點的作法看起來會更有效率。
藉由電阻式負載加到線性變阻器的觸點上來改變特性曲線是一個傳統上常用的技巧,通常負載電阻的大小大約為線性變阻器總阻值的1/20,在線性化數位式變阻器上加上如此負載的兩個缺點是,變阻器輸入阻抗受到增益設定影響在最大音量時為最小,同時端對端電阻值的寬廣變動範圍代表了左右聲道間的相互追蹤能力會在兩端之外的地方降低,圖四提供了這個概念。
圖五中的電路提供了傳統音量控制的特性,和圖三相當類似,不過它使用了一個較小的正回授來將可用範圍內的步階大小統一在大約每步階1.6dB,一個立即且明顯的缺點是,負回授分數必須為0.5或更高以便取得可用的結果,雖然0.25可能是穩定度的限制,這代表了已經捨棄了大約一半的可用設定碼以便讓電路能夠有效運作,不過餘下的17個設定碼則都被使用,並沒有像圖三中存在間隙,請參考表二,其中第三欄為了步階大小的變化,顯示出它在主要衰減範圍內相當良好的一致性。圖五電路的曲線圖顯示了線性化的效應,其中Y軸為以dB為單位的增益,並在X軸上以接觸點編號繪製,與圖三比較,這個作法較佳,圖三中所標示的數值大約帶來3dB的步階變化以及11個設定值選擇。
(表二) 圖四電路的計算結果
控制碼設定 |
增益 |
(差異) |
控制碼設定 |
增益 |
(差異) |
16 |
6.88 |
|
24 |
-5.60 |
1.61 |
17 |
5.19 |
1.68 |
25 |
-7.32 |
1.71 |
18 |
3.60 |
1.59 |
26 |
-9.17 |
1.86 |
19 |
2.06 |
1.54 |
27 |
-11.25 |
2.07 |
20 |
0.56 |
1.50 |
28 |
-13.65 |
2.40 |
21 |
-0.93 |
1.50 |
29 |
-16.59 |
2.94 |
22 |
-2.44 |
1.51 |
30 |
-20.53 |
3.94 |
23 |
-3.99 |
1.55 |
31 |
-26.95 |
6.42 |
|
32 |
Fully off |
- |
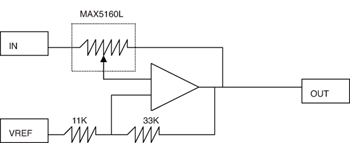
| 《圖五-a 每步階dB值變化接近一致的拓樸結構,經改善後的設計》 |
|
這個電路拓樸結構的一個副作用是在數位式變阻器的中間值會有6dB的提升,不過它可以在整個音訊處理路徑的增益結構中加以處理,事實上,在這裡基本上通常無可避免地需要進行一些增益位移的動作。
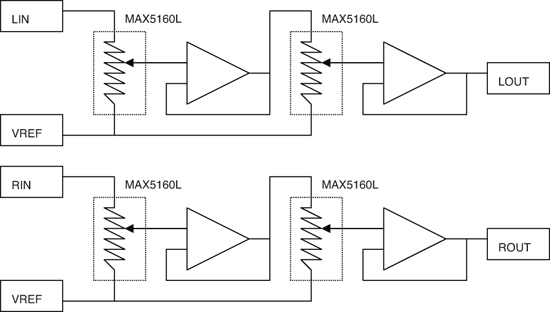
| 《圖六 傳統串接式立體聲音量控制,多就等於好嗎?》 |
|
圖六中的電路使用了總共4個MAX5160L來取得高解析度的立體聲音量控制,每通道的可用設定碼數目大幅提升,帶來32x32或1024個可用衰減設定碼,同樣地,端對端電阻值的容忍誤差因兩個數位式變阻器間的緩衝電路,因此不會有第一階效應,左右聲道間的相互追蹤能力則只受到接點間匹配精確度的限制,觸點電阻值的負載效應相當低,原因是每個觸點所面對的都是高阻抗的運算放大器輸入。
在1024個設定碼中,部分會提供重複的衰減值,例如第一個變阻器為-6dB,第二個無衰減,因此整體衰減為-6dB,而且如果其中一個變阻器設定為全幅衰減,那麼另一個電阻器的設定就沒有什麼意義,因此帶來大約由0到-60dB(實際為-59.66dB)約348個不同的衰減值設定,要將這些設定碼對應到衰減特性,可以使用模擬或試算表的方式,圖七顯示了所取得的衰減選擇分布,其中包含重複值:
圖七顯示了大部份設定碼的衰減值位於0到-40dB之間,每個衰減值間的dB步階變化可以以和表二類似的方式加以繪製,取得步階間隔的視覺化圖形。
步階間隔看起來分佈相當平均,大部份步階的差距都在0.5dB以下,只有在-41.6dB時達到1dB,以及接近終點的-53.6與-59.6間達到6dB,其中重複設定碼在圖中的差異為0,得到大部份專業級音量控制所需的控制範圍和級距。
不過這個作法也有它的限制,相當明顯的,這個電路的控制過於複雜,或許是使用查找對照表來取得數值並使用某些範圍演算法來取得平順的音量變化,但和圖二不同的是,再也不需受到穩定條件的限制,因此任何設定碼的組合都可行,嚴格來看,第一個和第二個數位變阻器間接點間的匹配誤差代表了無法保證單一性,僅使用部份設定碼,也就是步階變化較為粗糙可能是一個確保單一步階的方法,但是卻必須攜牲較精密的步階變化。
理論上來說,圖六中的電路乍看之下好像可以得到相當不錯的結果,但在實際導入時卻可能會面臨原先沒有預料到的問題。
結論
對大部份情況而言,圖三與圖五的電路可能帶來最佳成本、複雜度以及效能的最佳平衡選擇,使用3線式串列介面控制,Maxim也提供有MAX5400/1/2等元件選擇,它們提供需要較高解析度應用256個接點,並透過3線式通訊協定進行控制。
---本文作者任職於美商美信(Maxim)公司---

