取樣抖動指的是音頻信號穿過具有抖動的類比到數位轉換器(ADC)、數位到類比轉換器(DAC)、或者是異步取樣速率轉換器(ASRC)時,取樣信號在時間上變化的情形。前面兩者通常會和一個顯著的取樣時脈信號相配合,不過,ASRC就可能完全是數值的處理,其行為就像把原來的取樣時脈,再重新建立一符合新的立即取樣:在這種情況下,這取樣時脈是個虛擬的取樣時脈。
在很多情況下,取樣時脈必須由外部來源來取得。舉例來說,在一般家庭環境裏,如數位音頻錄音機或是數位環繞處理器,其DAC取樣時脈是從數位輸入數據串所取出來。對於專業的應用上,也有與DAC相關的裝置,例如,在這些應用上,ADC的取樣時脈需要與外部的訊號同步,或是數位串需要使用ASRC,再同步化到不同的參考值。
由於外部來源經常是會有抖動的情形發生,我們可以去觀察,測量並加以註解。不過,這並不是取樣抖動。這外部來源對於取樣時脈的抖動會有貢獻,但是那貢獻取決於外部來源的連接,與實際(或是虛擬)的取樣時脈間的時脈恢復電路(或是數值運算)的特性而定。這在它的行為上會顯現出本質抖動、抖動衰減及本身非線性行為。
時域區域模式
首先,先看在時域中的取樣抖動。如(圖一)所示,取樣在錯誤的時間,對訊號被轉換所造成的影響,會造成所謂的振幅誤差。除了DC信號外,任何訊號的振幅都會對時間做出改變,而且錯誤的取樣會立即產生振幅誤差。在(圖一)中,振幅誤差或是音頻信號的斜率成一定比例的改變,而這信號在高振幅高頻率的信號中誤差是最大的。
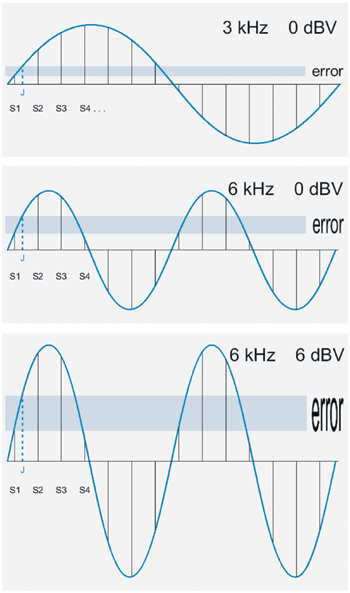
| 《圖一 不同振幅與頻率的信號,抖動取樣值J的變化》 |
|
在(圖一)這三個例子中,取樣頻率是固定的,只有變動訊號的頻率及振幅,注意當信號的振幅與頻率改變時,抖動取樣值J的變化
(圖二)顯示,隨機取樣抖動對一個純音調的影響。該圖中,音調為2V rms的振幅及1 kHz的頻率,誤差信號10 ns rms是利用隨機的Gaussian抖動振幅所計算出來的。圖中所產生的抖動模擬,是在176.4 kHz的取樣頻率時,對每個取樣誤差所計算出來的,這代表CD player是在4X倍頻取樣DAC訊號。
如(圖二)所示,取樣抖動在訊號1KHz,其信號的誤差信號是Jitter所引起,值得注意的是誤差信號及音調的交互調變,由於這誤差的產生,是由音調的斜率及抖動所造成,所以當音調在峰值時,其斜率是平的,此時,會有最低的取樣抖動誤差。
均方根(rms)誤差經模擬計算為124 (V rms,或是-84 dB(音調為2V rms)。假設這誤差是在176.4 kHz的取樣頻率中,平均地分散開來,遍及88.2 kHz頻寬,就可以估算出超過量測的音頻頻寬20kHz的雜訊程度大約是60(V rms,這時音調的大小約低於-90.5 dB。
該分析抖動影響的方法,可以被用在任何形式下,估算出可以接受的抖動程度。可以被簡化計算抖動的程度,如果是應用在「最壞情況」的信號,將會產生出振幅誤差,相當於區間的量化。例如,在一個16位元系統中,最壞情況-滿刻度20KHz的正弦波,會有個最大的斜率:
where
F=20 kHz 音調頻率
A=2 15=32768 LSB 音調振幅(峰值)
從這裡可以推論抖動程度不應該比243 ps峰值還大,但是這限制相當武斷,因為這對於1 LSB振幅的誤差並沒有任何關連,只與可聽度的誤差有關而已,不過這將會與頻譜內容的誤差有關連。
頻率區域模式
另一個觀察抖動影響的方法,是將它看做是一個調變過程,及以頻率來分析。它可以用數學的方式來表示,這是一個簡單的關係,存在於抖動頻譜元素、音頻信號頻譜元素、及有效的抖動調變結果之中。
如果信號在即時取樣時有誤差,導致信號立刻被調變,這可以用數學式來表示,如(公式一)所示。輸出信號( (t)是輸入信號時間的取代版本,而這位移的變化就是抖動。
其結果可利用正弦曲線抖動的頻率(j及峰對峰振幅J來做進一步分析。

| 《公式二:(t=j(t)=J/2(sin((j t)》 |
|
若輸入信號是餘弦波
則將上述的公式結合後,再重新排列,
![《公式四:((t)=A cos((i t) cos[ J(i /2 *sin ((j t)] ( A sin((i t) sin [J(i /2 sin ((j t)] 》](/art/2002/11/051643000081/F5.gif)
| 《公式四:((t)=A cos((i t) cos[ J(i /2 *sin ((j t)] ( A sin((i t) sin [J(i /2 sin ((j t)] 》 |
|
抖動振幅通常是小於10 ns,比信號週期(音頻的週期一般大於40000 ns)小很多。由於它本身抖動調變的程度非常小,在這樣的條件下,我們可以運用以下小角度的近似值:
![《公式五:cos [J(i /2 sin ((j t)]≒ 1》](/art/2002/11/051643000081/F6.gif)
| 《公式五:cos [J(i /2 sin ((j t)]≒ 1》 |
|
及
![《公式六:sin [J(i /2 sin ((j t)]≒J(i /2 sin ((j t)》](/art/2002/11/051643000081/F7.gif)
| 《公式六:sin [J(i /2 sin ((j t)]≒J(i /2 sin ((j t)》 |
|
帶入(公式四)後,就變成:
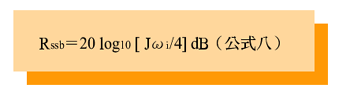
| 《公式七:((t)=A cos ((i t) ( A J(i /4 cos ( ((i -(j ) t)-A J(i /4 cos ( ((i + (j ) t) 》 |
|
從(公式七)可以得知,輸出信號因為抖動頻率的關係,所以除輸入信號頻率外,會有2個其他頻率相對於主頻的信號,而且它們的振幅是與抖動振幅及信號頻率產生有關;這結果可用來評估,因抖動調變所產生的聲音潛在可聽到的程度。
(圖三)表示抖動在實際信號上的影響。當圖中輸入信號為10 kHz,及抖動調變為3kHz時,會有兩個頻率相對於輸入信號,彼此間有3kHz的偏移,它們就是較高及較低的抖動調變邊頻帶。圖中,在頻譜上,靠近10kHz頻率時,雜訊會增加,形成所謂的「裙帶」;這些現像是在系統中,一些低頻率像雜訊的抖動所造成的。
信號對每個「單一」邊頻帶的比例,通常是以dB為單位。
![《公式八:Rssb=20 log10 [ J(i /4] dB》](/art/2002/11/051643000081/F9.gif)
| 《公式八:Rssb=20 log10 [ J(i /4] dB》 |
|
該結果是針對正弦抖動頻率,利用Fourier分析後所得到的結果,若更複雜的波形出現時,可以分成幾個正弦曲線頻率而且公式可以被應用。
為了簡便,公式可以簡化成兩邊頻帶的大小相加來當總誤差,然後用rms來表示抖動程度的大小Jn,以十億分之一秒來表示,及頻率(i,用kHz表示:
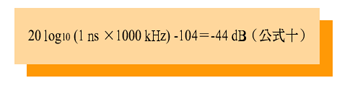
| 《公式九:Rdsb=20 log10 (Jn (i)-104 dB》 |
|
ADC /DAC結構之影響
在轉換器上的抖動影響會是比較複雜些,就如同上面音頻信號時間調變所討論的那樣。其他信號(例如,在noise shaping低位元轉換器中,所產生的高頻雜訊)可以與想要的音頻信號一起被取樣;在一些例子中,其他的調變過程也可能會發生。
超取樣轉換器
超取樣轉換器(Oversampling converters)不同一般轉換器的地方,在於取樣過程,其取樣的頻寬比起系統所需的最低速率頻寬,還要多出許多。典型的超取樣速率可以從2倍到256倍。較高的速率可以用noise shaping 方式,這技術對於提供低成本、高解析度的轉換是很重要的。(noise shaping可以產生分離影響,這部分後面再說明)。
因為在取樣時脈中的抖動頻寬,可以延伸到轉換器取樣頻率的一半,所以,與非超取樣轉換器比起來,抖動在一個超取樣的轉換器中,會被分散在較寬的頻譜。這誤差的造成是與抖動調變的抖動頻譜有關;因此,超取樣轉換器的誤差信號,也是擴散在較寬的頻譜。
在一個實際的例子中,假設1kHz信號,很均勻的被像雜訊般的抖動,每隔1ns來對頻譜做取樣,經過計算後,將會產生一個低於該信號的104dB誤差。
在(圖四)中,以4X超取樣DAC,該誤差信號將會被分散開來,比1X轉換器頻率範圍還大4倍。針對音頻方面,限制在20 Hz到20kHz寬頻,及量測超過該範圍,所以,音頻部分只包含全頻譜誤差雜訊的1/4功率。1/4功率代表著1/2的電壓,所以會低於一般非超取樣轉換器6dB的誤差。
不過,一般來說抖動來源並不是很平坦,由於振盪器的典型相位雜訊頻譜,及在時脈恢復電路中共用的低通抖動過濾,使得抖動經常是被較低的頻率元素來影響。而超取樣並不會降低低頻率抖動的衝擊。
Noise-Shaping與一位元的轉換器
高速率的超取樣技術,因為在對信號做量化時,會造成雜訊落在音頻頻帶之外,這有可能會降低位元數。換句話說,這技術雖然有很多優點,但是它卻產生了所謂的超音波雜訊-即超過音頻以外的雜訊。這雜訊程度與量化區間有關,對於一位元轉換器,總雜訊是接近於轉換器的全刻度的程度。
對於在超音波雜訊所產生調變的產品上,取樣抖動的作用,和它在音頻信號調變一樣。這些調變產生可以在音頻頻帶範圍內,也可以像是超音波雜訊存在那樣,即使是當音頻信號在低階,也不會有任何利於掩飾的效果。這影響會提升雜訊的最底部程度,並且降低轉換器的動態範圍。
說明這問題,我們舉一個例子來說,考慮超音波雜訊是在64X超取樣48 kHz delta-sigma轉換器中所產生,(在這例子中,ADC或是DAC,哪一個都無所謂)超音波雜訊是以高於音頻頻帶為開始點,然後到達取樣速率的一半,約1.5 MHz。對於取樣頻率在1000K、1 ns rms抖動時,這公式暗示著調變影響是連續的,如(公式十)。

| 《公式十:20 log10 (1 ns ( 1000 kHz) -104=-44 dB》 |
|
由於這雜訊分佈頻帶到達1.5 MHz,所以相對的這程度在音頻頻帶範圍內會比較小些。與平坦的抖動相比,它大概會小於20 dB,但是它到達至少抖動頻譜1/(特性,所以這減少有可能會增加到40 dB,會使得雜訊底部到達差不多是-84 dB FS。
Noise-Shaped轉換器因抖動所造成的音調
這裡發現有一個有趣的現像,在noise-shape一位元轉換器的輸出可以觀察到一個很低的音調。這DAC並沒有使用任何以上的技術,來降低取樣抖動敏感度,只是使用一個低抖動石英晶體的VCO,來確認在取樣時脈上的任何抖動是在非常低的。這些音調出現與VCO控制電壓的調變是相關的。但是,當在較高速度及低失真op-amp被使用在後極當過濾器時,這些音調卻又停止。
所以可以推斷當使用較低的性能op-amps時,會影響解調抖動,進而產生的超音波雜訊,而抖動是非線性。由於這調變類似於相位調變,所以與其說是振幅調變,倒不如說一些非對稱介於較高與較低間的邊頻帶。這抖動調變產生較高及較低的邊頻帶,都是在相反的相位。如果其有相同的振幅,在解調時就可以取消。
正常來說,在沒有信號時,抖動是不會產生任何的音調,但是如果抖動本身是音調的話,那麼調變邊頻帶就可能會產生音調,但是必定是調變信號的邊頻帶。