全球定位系統（Global Positioning System；GPS），是當前全世界最普及的全球導航衛星系統（Global Navigation Satellite System；GNSS），GPS總共放置了多達32顆高度位於地表20200公里以上的衛星，均勻地分佈在六個以55度傾斜於赤道的軌道面上。如此的設計提供高度的全球覆蓋度，並使得幾乎每一位使用者，在沒有任何遮蔽物阻擋訊號的條件下，都可以擁有至少四顆以上的衛星在可視範圍中以供定位之用。

GPS原先是由美國在20世紀中葉為了軍事相關用途所開發，然而隨著2000年5月美國柯林頓總統宣佈關閉選擇式供應（Selective Availability；SA）所造成的人為誤差後，定位誤差在一夕間從一百公尺降低到十幾公尺，大開GPS方便應用之門。現在GPS已被廣泛應用在其他領域，例如測量科學、航空安全、汽車及行人導航等，現今更成為許多手機的標準配備。GPS會如此盛行的另一個主因就在於它可以提供高精確度， 卻不向使用者收取服務費用。

與傳統AM及FM廣播系統類似，GPS也是從衛星到地面接收機的一種單向傳輸。與廣播系統的差異在於GPS接收機並不只靠單接收以及處理一個衛星的訊號就可以完成定位，相反地，需要同時收到來自多顆衛星的訊號。透過還原隱藏在傳輸訊號中的導航資訊，接收機方可得到定位所需的兩個重要資訊：首先是衛星的位置，接著是衛星到使用者的距離。有了超過四顆衛星的位置以及他們到接收機的距離估測之後，接收機便可以運用這些估測值來進行處理及決定其本身的位置、速度、以及時間（Position、Velocity、and Time；PVT）。一般說來，如果一個接收機可以掌握越多衛星訊號，則其對於位置估測的精確度便可以提高。然而實際上，並非所有的可視衛星皆可被成功接收。其主要的原因在於不同的衛星對於使用者有不同的仰角，導致信號的衰減或是接收訊號的強度並不一致，如果再加上使用者所在環境遭到建築物或是其他物體遮蔽，都可能會造成有部份衛星訊號強度降低到接收機無法成功接收。在冷開機（cold start）的情況下，要知道究竟有哪些衛星可供利用，便得透過複雜且費時的搜尋過程，因此降低搜尋時間或是運算複雜度的方法就變的相當重要。

除了美國GPS定位系統外，歐盟也於近幾年自行積極發展衛星導航定位系統，命名為伽利略衛星導航系統（Galileo），並於2006 年初開始透過第一顆實驗衛星（GIOVE-A）成功傳送Galileo衛星訊號，第二顆實驗衛星（GIOVE-B）也於2008年4月成功發射，未來歐盟將陸續發射總共達30顆衛星（27顆工作衛星與3顆輔助衛星）於3個軌道面上，並預計從2013年開始提供服務。

有別於GPS，Galileo有兩項特色，第一，其設計的初衷就是為了提供給民間廣泛使用，與美、俄導航定位系統原以軍事用途不同，因非軍事用途之故，Galileo不受戰爭影響，政治力介入少，並以相容於現存GPS與GLONASS為目標。第二，Galileo運用30顆衛星，每10個均勻分佈在三個軌道，定位誤差可小於1公尺，可補足美國GPS誤差達10公尺的缺點，更適合用於導航定位精確度要求高之應用，如緊急救援、飛機與船舶等。另外，Galileo衛星距離地面 24126公里，距離較GPS高，且軌道面比GPS更偏向赤道，故定位訊號傳送可覆蓋更廣的區域。歐盟發展此系統，並與中國合作，除看好導航定位的潛在市場需求外，不讓美國系統的GPS專美於前亦為重要的因素之一。Galileo部分功能優於GPS，如較低的誤差範圍及更廣域之訊號，成為GPS以外的另一項定位系統選擇。但另一方面，基於民間用途，Galileo未來發展是以相容於現存GPS與 GLONASS為目標，是以互補關係為主。當GPS及Galileo完成建構之後，將可擴大全球的衛星涵蓋進而增進可視衛星數 目，定位的精準度也可望大幅地提昇。

訊號格式

GPS

《圖一　GPS C/A碼訊號格式示意圖》

GPS衛星訊號的調變方法主要是基於二進位相移調變（BPSK），並利用分碼多工（CDMA）的機制來作衛星區別。圖一中，首先導航資訊以50bps的速率傳送，意味著每一資料位元傳輸所需的時間為20ms，接著數位資訊都將在時域上乘上一組特別的C/A（Coarse/Acquisition）碼[1]。GPS的C/A碼共含有1023個chips，以1.023Mcps的碼速率傳送，因此每個C/A碼的週期為1ms，且每一個chip的長度為977.52ns或者代表大約300m的距離長度（考慮光速為3×108m/s）。如果一個接收機以16倍碼速率的速度做數位取樣，則理想上時序可以達到1/32的碼同步誤差，換算成距離誤差大約就為10m左右。

回到圖一，任一個導航資訊位元，將會包含著20個重複的C/A碼。注意如圖所示，C/A碼的訊號邊緣與導航資訊位元是對齊的，因此，接收機便可以透過同步C/A碼的方式來找到導航資訊位元的訊號邊緣。當導航資訊與C/A碼相乘之後，透過升頻的方式將訊號載波到L1頻帶（1575.42MHz）然後廣播到地球。目前，C/A碼只有在L1頻帶上傳送，有別於針對軍事上用途的P（Y）碼（precision code），在L1以及L2頻帶（1227.6 MHz）上都有其訊號的成份。

Galileo

Galileo在幾個不同頻帶都有傳送訊號，由低頻到高頻分別是E5a（1176.45MHz）、E5（1191.795MHz）、E5b（1207.14MHz）、E6（1278.75MHz）、E1（1575.42MHz）[2]。其中E1頻帶與GPS的L1頻帶重複，因此本文將只討論Galileo在E1頻帶上提供的開放式服務。與GPS提供的服務類似，其導航碼也跟C/A碼一樣是完全公開。與GPS不同，Galileo將其發送的訊號分成兩個不同的通道做傳輸，分別命名為資訊通道E1B以及導引通道E1C。在導引通道裡面，並不包含任何導航的數位資訊，真正可以用來導航的資訊只放在資訊通道上，導引通道的引入使得訊號在擷取及追蹤都更容易。另外，Galielo傳送的導航資訊都將會額外經過交錯、以及在前向錯誤更正碼中的迴旋編碼進行處理，進一步增強訊號的偵錯能力。

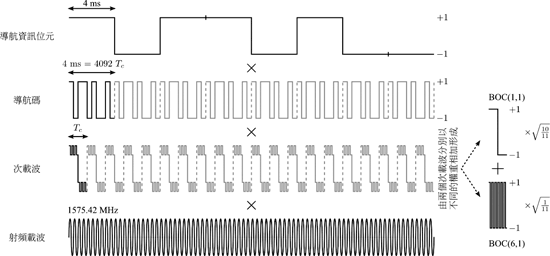
《圖二　Galileo E1B資訊通道的訊號格式示意圖》

參照圖二E1B的傳輸訊號，可以發現導航資料位元的傳輸長度與GPS比較，從20ms縮短成4ms，與此同時，導航碼則是增長到4ms，因此對於E1B來說，一個導航資訊位元將包含一個完整週期的導航碼。與GPS一樣，導航資訊位元與導航碼的起始位置都相同，因此位元邊際都是互相對齊的。E1B的導航碼共包含了4092個chips，使用與GPS的碼速率相同的1.023Mcps的速度傳送。與GPS系統最大的差異則是Galileo引進了新的調變方式，稱多工二進制偏移載波調變（MBOC）。如圖二所示，E1B的訊號除了將導航資訊乘以導航碼之外，還要再多乘一個次載波信號。這個次載波由兩個二進制偏移載波BOC（1,1）及BOC（6,1）分別乘上正規化因子√(10/11)跟√(1/11)之後相加所組成，因為Galileo的次載波都是以這種方式形成，所以又被稱為複合二進制偏移載波（CBOC）。在圖中BOC（m,n）的表示法主要是用來描述次載波頻率為m×1.023MHz且碼頻率為n×1.023MHz。所以可以看到在BOC（1,1）中一個chip有一個完整週期的正弦方波訊號，而BOC（6,1）即代表著六個正弦方波訊號存在於一個chip內，顯而易見的，BOC（6,1）的高頻成份比BOC（1,1）更多。這一點也可以在接下來的功率頻譜密度函數中看出來。

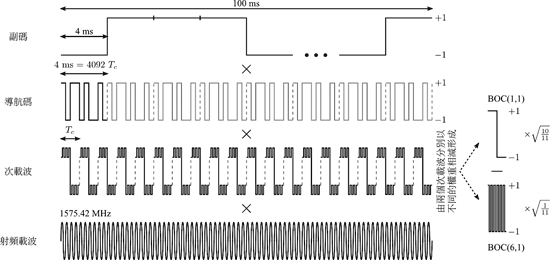
《圖三　Galileo E1C導引通道的訊號格式示意圖》

至於E1C的部份，如圖三，由於其不需要負責傳輸任何導航資訊位元，取而代之的是一組固定的副碼，其單一位元長度為4ms，一共有25個位元，所以總共長度為100ms。另外在次載波組合上也有些微的差異，在E1B上次載波為BOC（1,1）與BOC（6,1）乘上相對應的正規化因子後相加而成，反之，E1C上的次 載波則是由乘上正規化因子的BOC（1,1），減去乘上正規化因子的BOC（6,1）組合而成。

碼自相關函數及功率頻譜函數

一個展頻碼c[n]的自相關函數r[n]可以表示成：

《公式一》

其中，Nc為碼長度。在圖四以及圖五中，分別針對GPS C/A碼以及Galileo E1B的導航碼，繪出他們的自相關函數特性。從圖中大略可以知道，一個好的展頻碼所必須具備的特性，就是自相關函數在兩兩訊號非同步時候的大小，必須盡量保持在與信號同步的時候有較大的差異。事實上，一般接收機也正是利用這個特性來做訊號同步。假設收到訊號的取樣為x[n]，則透過交互相關值的測量 ：

《公式二》

其中，N為同步積分的長度，一般來說設計在碼長度的整數倍。當交互相關的測量值大於某一設定的閾值時，接收機就可以基於當時測量的碼相位去作訊號時序上面的同步。由於C/A碼其實就是金氏碼（Gold code）的一種，所以可以看到圖四除了主峰值之外，C/A碼的自相關函數在其他位置的大小只有三種可能，反觀圖五Galileo E1B導航碼的自相關函數，由於其產生是基於一種記憶碼，其在峰值之外的大小分佈也比較不均勻。

《圖四　GPS C/A碼自相關函數》

《圖五　Galileo 導航碼自相關函數》

如果對峰值左右各一個chip的時間範圍作放大，可以得到如圖六的波形。GPS的自相關函數在峰值附近呈現出一個三角波，而Galileo則比較陡峭，且除了主峰外還有兩個高度較低的側峰。波形改變的原因，主要是因為Galileo引進了次載波的調變，導致自相關函數以更快的速度向兩邊衰減至零，然後分別走至兩端的負向側峰。主峰寬度變窄主要的好處是導航距離誤差的下降，這是由於在常用的信號追蹤過程中，一個越陡峭的主峰可以在碼鑑別函數中產生越陡峭的S曲線，進而降低雜訊的影響，提昇訊號追蹤準確度。

然而，隨著主峰寬度變小，訊號擷取也更加困難。因為一般接收機在訊號擷取過程中，採用固定碼相位間距去測量每個碼相位上的相關函數值大小，以判定是否擷取到正確的訊號相位，所以主峰寬度越小，碼相位搜尋間距也需要隨之變小，以確保可以取樣到主峰所在的碼相位，且維持足夠的訊噪比。然而間距縮小意味著在一個碼週期裡頭，所需要測試的碼相位變更多。如此將造成計算複雜度以及硬體成本的增加。

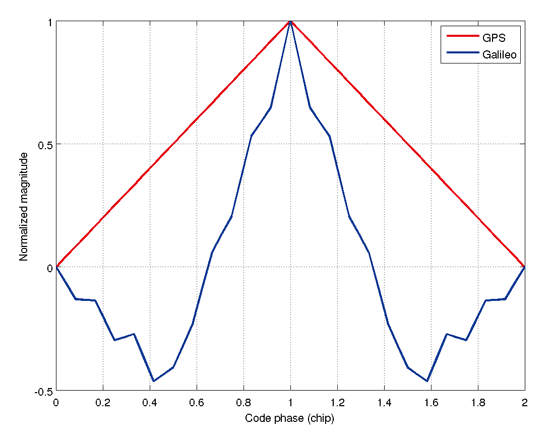
《圖六　GPS C/A碼與Galileo 導航碼之自相關函數在峰值附近的放大圖》

圖七模擬產生GPS C/A碼及Galileo E1B導航碼的功率頻譜密度函數，因為C/A碼的碼頻率為1.023Mcps，所以造成如圖上類似sinc2的頻譜，其零點到零點的頻寬為大約2MHz。反觀Galileo的頻譜，由於次載波調變的緣故，其頻譜從中間向兩旁偏移，與GPS頻譜重疊的部份減少，因而，兩個系統彼此的互相干擾也可以有效降低，這也是另一個採用次載波調變帶來的優點。這種頻譜偏移現象其實類似把一個基頻訊號乘上一個載波調變到高頻，只不過對於Galileo來說，乘上的這個次載波在基數倍碼頻率的位置都有能量存在。所以可以看到因為BOC（1,1）這個成份造成在1、3、5、7MHz左右有比較大能量的情形，而BOC（6,1）則導致在大約6MHz附近也有峰值的現象。此外，從頻譜的資訊中也可以估計出要接收到主峰的訊號成份所需要之最小頻寬，對於GPS來說是2MHz，Galileo是4MHz。

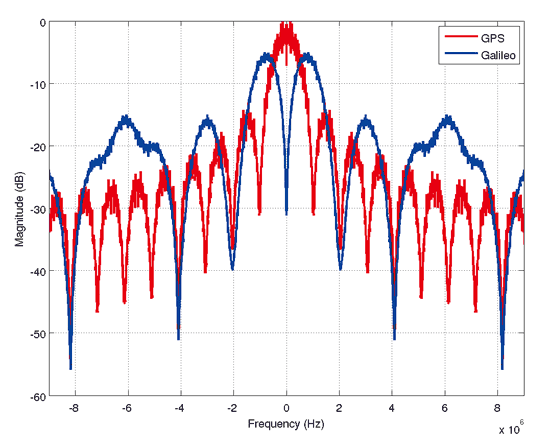
《圖七　GPS C/A碼與Galileo 導航碼之功率頻譜密度函數》

信號擷取

基頻接收機架購

為了取得接收機的位置，基頻的電路有三項主要任務：擷取、追蹤、及導航。信號擷取的目的在於判定其可以掌握的衛星數量及衛星號碼。為了決定哪一顆衛星是否要先作搜尋，通常會使用衛星搜尋演算法以決定哪一顆衛星有較高的出現機率。在完成信號擷取的程序之後，對於掌握到的衛星其頻率以及碼相位估測誤差通常都不大，不過因為頻率及碼相位的誤差皆非定值，因此接收機必須利用在信號擷取中所獲得的資訊作訊號追蹤，此程序會進一步改進前述兩項估計值的精確度，直到估計值相對穩定下來後，才會把碼相位的資訊及已經解調的導航資訊位元輸出給後端的導航模組。

圖八為一個典型的基頻導航接收機主要的模組方塊圖，中頻的訊號在數位取樣過後，送到訊號擷取的通道去作處理，一般接收機為了加速搜尋衛星的速度，均採用多套擷取模組同時處理多顆衛星的搜索方式。在每一個擷取通道中，訊號因為都卜勒效應所造成的頻率漂移會先被估測，為了考慮接收機本身的振盪器漂移，正負10kHz的搜尋範圍是一般常用的設計值。為了加速頻率搜尋的速度，在這個區間裡頭等間隔頻率（如500Hz）將由頻率數控震盪器產生出來。當接收訊號的頻率誤差被補償回來之後，接著便是要去估計碼相位，這部份由碼數控振盪器產生的本地端複製碼，會跟接收的信號作交互相關偵測，其結果就像圖四與圖五所示。當本地端的複製碼跟接收訊號同步的時候，後端的相關性峰值驗證將會依據事先決定的閾值判斷此峰值所代表的碼相位是否正確，如果相關值小於閥值，擷取通道將會持續改變都卜勒以及碼相位的參數，如果所有可能的參數都已經測試過且都未能超過閥值，此時，接收機便判定目前搜索的衛星不存在或是訊號太弱，因此擷取通道將會再尋找下一顆可能出現的衛星。

《圖八　導航接收機之基頻架構模組》

時域上匹配濾波器

如前所述，在任何一個擷取通道中，必須對收到訊號的都卜勒頻率以及碼相位作估測的動作。搜索頻率及碼相位的過程可以用圖九來做進一步的說明。在圖中 二維平面上每一個小方格代表待測試的都卜勒頻率及碼相位。在導航的訊號擷取中，碼相位所需要測試的數量會遠大於都卜勒頻率，以GPS的 C/A碼為例，考慮在訊號擷取時採取的頻率解析度為500Hz及碼解析度為1/2 chip，則接收機所需要測試的都卜勒頻率分別為0、±0.5、±1、...、±10kHz共41組。但所需要測試的碼相位卻高達2046個。在Galileo的訊號中，因為碼長度增為四倍及碼解析度需求更高，這個差距將變得更大，因此一個快速搜尋碼相位的演算法就更為重要。

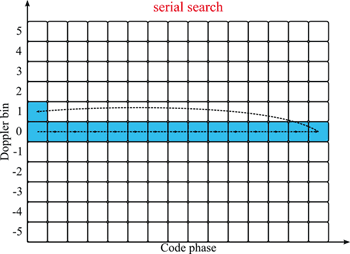
《圖九　序列式搜尋法在都卜勒頻率：碼相位之二維搜尋平面之示意圖》

圖十所示為一個基於匹配濾波器所實現，可用來測試碼相位的快速相關器，可看到上下各有一長串的暫存器陣列，分別存著接收到的訊號取樣點以及本地端的複製碼，在本裝置正式估算碼相位之前，複製碼將透過碼數控振盪器，根據目前所欲搜尋的衛星碼產生並依序輸入碼暫存器陣列中，直到複製碼完全被讀取。此時，一個完整週期的複製碼取樣將會存在下方暫存器中。反觀上方的暫存器收到的訊號，隨著每一次clock的驅動，新的取樣值將存入暫存器、舊有的取樣點各自往前移動到下一個暫存器、最後的取樣點則會消失在暫存器陣列中。因此可以發現， 本地的複製碼是固定的，只有收到的訊號在暫存器中移動，造成彼此所對應的相位差也持續在改變。所以只要在一個碼週期的時間過後，這個匹配濾波器便可以輸出 所有的碼相位估計值。事實上，在每一次的clock驅動中，一個所對應的碼相位估計就會被輸出，後端的驗證模組也可以立刻判斷相關值的大小。這種在固定一個都卜勒測試頻率下依序測試每個碼相位的搜尋方式，又稱為序列式搜尋。

《圖十　運用匹配濾波器作訊號擷取》

《圖十一　運用傅立葉轉換作訊號擷取》

頻域上傅立葉轉換

隨著快速傅立葉轉換（FFT）演算法的成熟發展，對比在時域上計算碼相位相關值的方式，將訊號藉由FFT轉到頻譜域上面作處理的想法也被提出[3]。其主要的精神是，在時域上作相關值的運算與迴旋積分十分類似。而時域上兩函數的迴旋積分等同於在頻域上作相乘。如圖十一所示，將接收到的訊號先去除其殘餘的都卜勒頻移，然後作傅立葉轉換，與本地複製碼傅立葉轉換後的共軛複數作相乘，再透過IFFT轉換到時域上，IFFT輸出的資訊即代表了碼相位的相關值大小。由於傅立葉轉換演算法的進步，使得計算複雜度下降，因此在軟體接收機上，在頻域上用傅立葉轉換的方式去作訊號擷取也比匹配濾波器的架構更受歡迎。由於傅立葉轉換的處理方式乃接收一段資訊後做區塊型的處理，因此採用這種搜尋方式為一種平行式的搜尋方法，如圖十二所示。唯區塊型的處理在實際應用上必須更小心處理資訊位元調變問題，以Galileo來解釋，因為每個資料位元的長度為4ms，如果處理的區塊剛好從一半2ms的位置開始抓取，則這收下來的區塊必定包含兩個位元的部份資訊。當兩個位元的極性一致時，也就是同為+1或是-1時，則沒有問題，但是當位元恰為反向時，則在做相關值計算時可以發現，即使訊號已同步，因為極性相反相關值的增益將互相抵銷，導致訊號擷取失敗，因此這也是傅立葉轉換必須額外注意的事項。

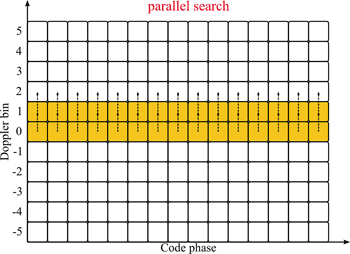
《圖十二　平行式搜尋法在都卜勒頻率：碼相位之二維搜尋平面之示意圖》

縮短測試時間訊號擷取演算法

前文提到，Galileo所使用的碼長度比起GPS C/A碼來說變成四倍，這不單只是增加訊號擷取的複雜度，也使搜尋碼相位所需的時間更長。本研究嘗試不使用跟收到訊號內含一致的複製碼，取而代之改變這個複製碼的形式，讓其可以更快擷取到衛星訊號。這想法源自於部份相關的方式以估測碼相位，然而部份相關估測法存在一個嚴重的問題，就是如果實際接收訊號的碼相位不存在這個部份碼的話，則接收機便會錯過可以搜尋到衛星的機會，除非有額外的驗證機制存在。為了改善這項缺點，我們提出了迴旋式位移後合併碼（cyclically shift-and-combine code；CSC）[4]。

《圖十三　CSC碼的概念與形成方法》

利用圖十三將這個概念簡單的呈現出來。在這個例子中，只單純考慮訊號時序上不同步的效應，其它例如雜訊、干擾、或是頻率不同步的非理想效應先忽略不計。假設展頻碼的週期為12個單位，數字標記為代表其所對應的碼相位，因為打算把原始的展頻碼縮短四倍，所以依序把展頻碼循環位移3個單位，總共位移3次。如圖所示，便可以得到四個除了起始的碼相位不同之外，其它特性完全相同的展頻碼，接著把這4個循環位移碼相加起來之後可以得到一個新的碼，這個新組成的碼會有四個連續重複的部份，因此只需要保留其中一段即可，並稱之為CSC碼。透過這樣的處理改變碼的形式，CSC碼的週期也縮短成原始展頻碼的1/4。

以圖中接收到的一段訊號來說明CSC碼仍舊具備擷取訊號的功能。這一段接收訊號的起始位置所對應到的展頻碼相位為2。圖中CSC碼第一個組成成份為0、1、2，將其向左循環式位移2個單位，則其2的成份可以與接收訊號對齊。再來看第四個組成部分3、 4、5，同樣地，其中3及4的部份在向左位移兩個單位後也可以與接收的訊號同步，至於其他組成的成份因為沒有等同的接受訊號與之對應，所以將不會對相關運算的峰值造成貢獻。如果把接收的訊號繼續往後看三個單位5、6、7，同樣可以歸納出這個結果，亦即當前接收到訊號的碼相位為CSC碼向左循環式位移兩個單位的碼相位。然而在此出現另一個須注意的事項：既然CSC碼中包含了原始展頻碼的四段成份，所以無法得知真實的碼相位是位在2、11、8、 5中的哪一個，因此，在使用CSC碼作訊號擷取的過程中，雖然可以縮短所需要測試的碼相位四倍，但是接收機隨後必須額外再去測試四個可能的碼相位。

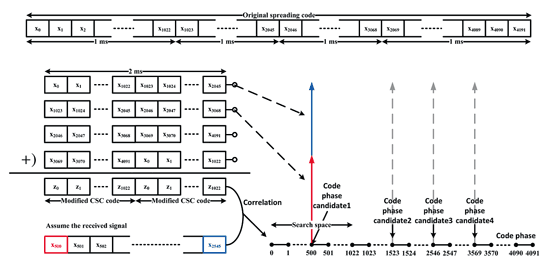
《圖十四　以Galileo的導航碼形成CSC碼的實例》

在圖十四中，以實際Galileo E1B的導航碼作測試，在這個實驗中，假設接收訊號的真實碼相位座落在500 chips的位置，因為原始的導航碼為4ms，所以CSC碼縮短成1ms，其中包含了1023的chip，為了維持峰值的相對高度以利於後端的驗證，接收2ms的長度作同步積分。由於CSC碼的特性，可以在相位偵測500 chips的位置發現峰值。但真正的相位碼偏移可能座落在500、500+1023、500+2×1023、500+3×1023 chips的碼相位上。從這個例子中可以發現使用原本的導航碼，接收機必須一一測試4092個不同的碼相位，不過經由CSC碼的幫助，可以將需要搜尋的碼相位降至1023個，即使加上額外4個碼相位的驗證，總共只需要1027個，因此可大幅降低所需的搜尋時間。

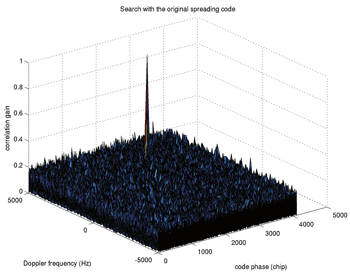
《圖十五　利用原始導航碼作訊號擷取之二維搜尋平面圖》

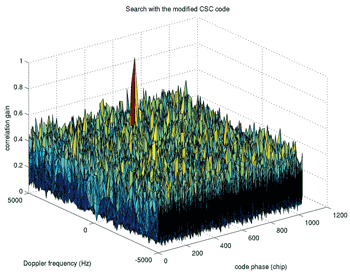
《圖十六　利用CSC碼作訊號擷取之二維搜尋平面圖》

圖十五、十六分別顯示原始導航碼以及CSC碼在二維訊號擷取平面圖所得到的模擬圖，在這個實驗中各項參數的設定如下：都卜勒頻率的偏移為2500Hz，接收訊號的訊雜比設定在45dB/Hz，同步積分時間為4ms。另外刻意把接收訊號的碼相位移至2546。再次從圖十六中看到CSC碼，可以正確在碼相位500的位置偵測到峰值，當然更進一步驗證其他四個可能的碼相位是必須的。接著從這兩張圖可以比較發現，使用CSC碼會造成峰值與非峰值之間的差距變小。會造成這樣的效應主要是因為在CSC 碼中，除了與接受訊號同步的區塊之外還有其他的部份，因為與接受訊號不同步，造成類似干擾的效應。

結論

本文回顧現今已經被廣泛使用的GPS系統，瞭解其展頻碼在自相關函數以及功率頻譜函數上的特性。同時也介紹了歐盟下一代的Galileo導航系統，以及其在同樣是1575.42MHz載波上的導航碼與GPS C/A碼之異同，隨著多工二進制偏移載波（MBOC）調變的引入，下一代的導航將可以擁有更精準的位置估測。但實際上其帶來許多設計上新的挑戰有待克服， 其中一個便是因為碼長度增加所造成的複雜度提昇以及搜尋時間變長。本文提出了新的想法以改變本地端複製碼的形式，可以大幅度的減少所需搜尋的相位，雖然使用本文的方法會造成訊號擷取上峰值的相對高度降低，然而，在多數室外應用場合衛星訊號的強度品質通常良好，這個時候便可以利用本文供的方法對存在的衛星作更快速地搜尋。

參考資料：