近來許多半導體製造商紛紛推出了擁有卓越性能的高速類比數位轉換器(Analog/Digital Converter;ADC)產品,因此您可能要問,「這些廠商是如何測量晶片的效能?又是使用哪些設備來作測量的呢?」以下我們就為您介紹在ADC轉換器中最重要的兩個精確度參數的量測方法,那就是積分非線性度(Integral NonLinearity;INL)以及微分非線性度(DifferentialNonLinearity;DNL)。除非常使用ADC產品,否則我們常會忘記INL與DNL這兩個參數的真正意義以及重要性,以下我們將先對這方面的定義做一個簡單的解釋。
INL誤差的定義為其實際轉換函
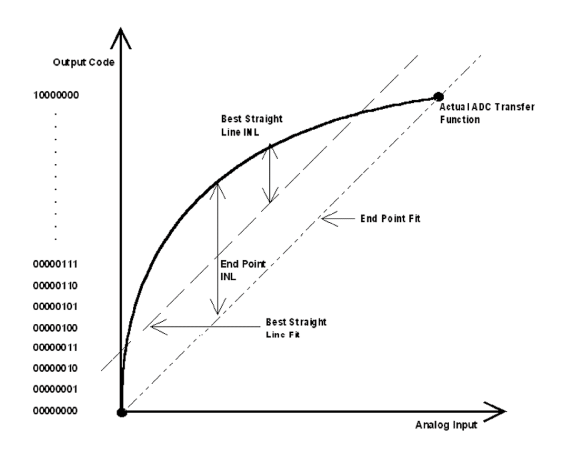
數與直線之間的誤差,以LSB或整個轉換運作範圍的百分比為單位,因此INL誤差量的大小就與直線所選擇的位置直接相關。我們常用的定義法有兩種,那就是「最佳直線(best straight line)法」與「端點(endpoint)法」,請見(圖一)。
最佳直線法提供了有關位移(截距)誤差、增益(斜率)誤差以及轉換函數位置等資訊,它以直線的方式來決定最接近ADC轉換函數的線性值,雖然直線的正確位置定義並不明確,但是這個方法卻可以提供最佳的可重複性,並且可以作為線性化程度的真正代表。
端點INL測量法則是以直線通過轉換器轉換函數的兩端點,因此可以定義直線的精確位置;也就是說,不管是幾位元的轉換器,直線都以通過輸出碼全為0的零輸出與輸出碼全為1的滿載輸出兩端點的直線所代表。不過這個方法卻可能因為增益與位移誤差而降低INL測量的準確度。
由於最佳直線法能夠產生較為精確的結果,因此比較常被使用。
如下面將要討論的INL的規格即是在增益與位移誤差被去除後所測量:
INL =|[(VD -VOFFEST)/LSBI DEAL - D|, where 0 < D < 2N-1.
其中VD為數位輸出碼D所代表的類比輸入值,N則為ADC轉換器的解析度,VOFFSET為輸出全部為零時的最低類比輸入,LSBIDEAL則為兩個相鄰數位輸出碼之間最理想的間隔。
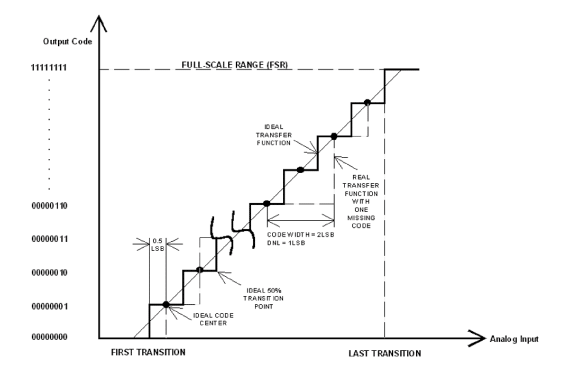
DNL誤差的定義是實際步階寬與一個LSB理想值之間的差距,請見(圖二)。
對DNL = 0LSB的理想ADC轉換器來說,每個類比間隔就等於一個LSB,而每個轉換點之間的間隔也正好是1LSB,擁有≦1LSB之DNL誤差可以確保擁有無跳空輸出碼,也就是每個碼都連續的單調(monotonic)轉換函數(基本上單調轉換函數的斜率從來不會改變符號),與INL一樣,DNL的定義也是在增益與位移誤差去除後所指定,它的定義為:
DNL=|[(VD+1- VD)/LSBIDEAL - 1]|, where 0 < D < 2N - 2.
其中VD為數位輸出碼D所相對的實際輸入值,N為ADC轉換器的解析度,LSBIDEAL為兩個相鄰數位輸出碼間的理想間隔,再加入雜訊與各種量化效應之外的寄生效應影響考量,較高的DNL值通常會限制ADC轉換器在信號雜訊比(Signal Noise Ratio;SNR)與無寄生雜訊動態範圍(Spurious-Free Dynamic Range;SFDR)上的性能表現。
| 《圖一 最佳直線與端點逼近法》 - BigPic:562x464 |
|
靜態INL與DNL測量的基本測試環境安排
INL與DNL可以採用準直流(quasi-dc)斜波電壓或者是低頻的正弦波作為輸入來加以測量。一個簡單的直流斜波測量會包含邏輯分析儀器、可選用的高精密度數位類比轉換器(Digital Analog Converter;DAC)、可以提供受測元件輸入範圍變化的高精度直流源,以及可以連接到個人電腦或者是X-Y繪圖機的控制介面。
如果在整個測試環境中包含了比受測元件精密度高上許多的高解析度DAC轉換器,那麼邏輯分析儀就可以透過處理ADC轉換器上的輸出資料來監測位移與增益誤差,精確的訊號源會在受測元件的輸入產生一個從零到滿載的緩慢變化測試電壓,當這些輸出碼由DAC轉換器重新還原為電壓值時,將它減掉受測元件輸入端的相對測試電壓值,就會得到一個可以在X-Y繪圖機上顯現的微小電壓差VDIFF,取得與INL及DNL誤差的關聯,在量化位準上的改變就代表了微分非線性度,而VDIFF與零之間的誤差就是積分非線性度。
加入類比伺服迴路
另一個與前面類似但更為複雜,用來決定靜態非線性參數的方法是在測試中加入了類比伺服迴路,這個方法通常用在較高精確度的測量,而非測量速度的考量。
一個典型的類比伺服迴路包含一個積分電路及兩個連接到ADC輸入端的電流源,請見(圖三),其中一個電流源提供積分電路所需的電流,而另一個則作為電流消耗,一個連接到ADC輸出端的數值比較器控制這兩個電流源,而這個數值比較器的另一個輸入端則連接到PC,可以依序產生2N-1個測試碼,其中N為轉換器的解析度。
如果迴路回饋的極性正確,那麼數值比較器將會使電流源在某個輸出碼轉換時提供類比輸入,理想上這個動作會在類比輸入端產生一個小的三角波,數值比較器則控制這些斜波的頻率與方向,積分器的斜率在接近轉換點時必須要夠快,但是卻又必須慢到足以在使用精確數位電壓表測量時能夠將這些疊加之三角波的短暫波峰值降到最低。
| 《圖二 ADC無漏空輸出碼,DNL須小於1LSB》 - BigPic:560x370 |
|
以MAX108的INL/DNL參數測試來說,伺服迴路電路板透過兩個接頭連接到評估板上,請見(圖四),其中一個用來建立起MAX108主要或附屬輸出埠與數值比較器可閂鎖輸入埠的連接,另一個則用來確保伺服迴路與由電腦所產生的數位參考碼間的連接。
由於由比較器輸出的完全解碼決定在於比較器輸出P > QOUT上,接著傳給積分電路的部份,每個比較的結果會分別控制開關的邏輯輸入,並且在需要時產生所需的電壓三角波以便驅動受測元件兩個輸入端的積分電路。
這個方法有它的優點,但同時也擁有以下的幾個缺點:
1.三角波必須要擁有較低的dV/dt變化以便將雜訊降到最低,這樣雖然可以產生可重覆的數出數值,但是卻會造成精確電表較長的積分時間。
2,正向與負向三角波必須要相合以達到50%的中點,而且這個低電壓的三角波必須在平均上達到需要直流位準。
3.積分器的設計通常必須小心選用充電電容,為了將電容「記憶效應」所帶來的可能誤差降到最低,最好選用擁有較低的介質吸收的積分電容。
4.精密度與積分時間長短成正比,但與所需穩定時間成反比。
一個連接到類比積分伺服迴路的電壓表可以用來量測INL/DNL誤差與輸出碼的相對關係,請見(圖五)與(圖六),請注意在「INL vs.輸出碼」圖中的拋物線或曲線代表偶數諧震波,而S形曲線則代表著奇數諧震波。
為了降低前述方法的負面影響,我們可以將伺服迴路的積分電路部分改用可以抓取受測元件輸出碼的逐次逼近暫存器(Successive-approximation Register;SAR)、L-Bit DAC轉換器以及一個簡單的平均電路來取代。配合數值比較器,這個線路可以形成一個SAR型態的轉換組態,請見(圖七)。在圖中數值比較器控制DAC,讀取它的輸出,並逐次逼近,同時DAC會在受測元件N-bit ADC的輸入端產生精確的直流電壓;在這裡,我們選用一個16-Bit的DAC來將ADC的精確度調整到1/8LSB,並且得到最佳可能的轉換曲線。
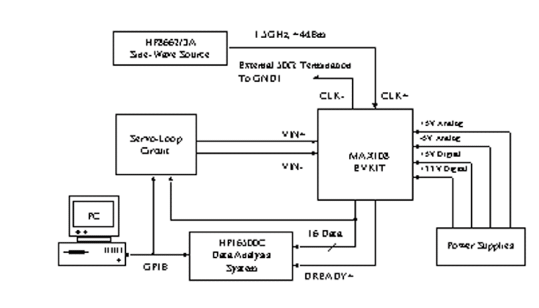
| 《圖四 此測試安排可以用來決定MAX108的INL與DNL參數》 |
|
平均電路好處在雜訊造成數值比較器來回震盪,或變成不穩定時特別有用,尤其在接近最終結果時,在平均電路中包含有兩個除法計數器,其中「參考」計數器擁有2M時脈週期,而M為控制時間長度的可變整數,只有在數值比較器輸出為高電位時才計數的「資料」計數器則等於最初2M-1週期的一半。
資料計數器只有在當數值比較器為高電位器時才進行計數的動作,而參考與資料比較器會將高電位與低電位發生的次數平均,將結果儲存在一個正反器內,並將它傳給SAR暫存器。
這個動作在這個測試中重覆16次以產生完整的輸出碼,就和前面所提到的方法一樣,這個方法也有它的優點和缺點:
1.這個測試的輸入電壓以數位方式定義,可以讓我們簡單地修改所需結果平均取樣的次數。
2.SAR的做法會在受測元件的類比輸入端提供一個真流位準而非斜波電壓。
3.缺點是在反饋迴路中的DAC會限制輸入電壓的解析度。
INL與DNL的動態測試
為了測量ADC的動態非線性度,我們可以加入一個全震幅的正弦波輸入信號,接著在轉換器的整個全功率輸入頻寬上測量轉換器的訊號雜訊比( Signal-to-Noise Ratioisnr),理論上一個理想N-bit轉換器的SNR,在只考量量化雜訊且無失真的情況下為:
SNR (in dB) = N*6.02 + 1.76.
在這個作法上包含有雜訊效應、樍分非線性度以及取樣時間不確定等性的考量,我們可以透過固定頻率下SNR的測量以及作為訊號振幅的函數取得更多的線性度資訊。在由零到滿載或滿載到零等逐漸改變整個振幅的大小時,將會因電源振幅接近轉換器滿載限制而產生較大的誤差,為了找出這些誤差的原因,同時去掉失真以及不穩定時脈的影響,我們應該使用頻譜分析儀來分析頻率函數的量化誤差訊號。
雖然還有其他許多的方法來測試高速與低速轉換器的動態與靜態INL及DNL參數,這篇文章最主要是讓有興趣的讀者對有關功能強大運作特性測試的進一步瞭解,以及透過使用簡單的工具與技術來取得精確測量度的聰明作法。
【名詞解釋】
1.轉換函數:理想的ADC的轉換函數為階梯狀,其中每一格代表特定的數位輸出碼,而每一個上升緣則代表兩個相臨數位碼之間的變化,這些變化的相對輸入電壓必須要能夠找出以便指定ADC的性能參數,這個步驟可能非常複雜,特別是在高速轉換器高雜訊的轉換,以及取得接近最後結果並且變換緩縵的數位輸出碼時。
在(圖二)中,轉換函數並沒有明確的定義,但卻以比較真實的機率函數來表示,當緩慢增加的輸入電壓通過轉換點時,ADC轉換器則更加可能變成下一個相臨輸出碼,在定義上,ADC轉換器在該輸入電壓時有相等的機率會輸出相臨兩數位碼中的一個。
2.正確的轉換:轉換電壓的定義為有相等機率會產生兩相臨數位輸出碼之一的輸入電壓,而平均的類比電壓值則定義這個範圍的中點,如果我們知道轉換區間範圍,那麼就相當容易取得這個50%的點,這個轉換點可以在測試時透過量測轉換區間的範圍,然後將區間除以在其中所出現輸出碼的數目來決定。
3.SAR轉換器:SAR轉換器的工作原理就是化學家所使用的天平量測法相近,其中一端為未知的輸入樣本,而另一端則為由SAR/DAC組態所產生的第一個權值,也就是最重要的位元(MSB),等於全幅輸出的一半,如果未知的輸入大於1/2 FSR,那麼就將第一個權值留下,如果小於,那麼就移除。
SAR轉換器透過這個程序,由MSB到LSB執行N次來決定所需的輸出碼,其中N為DAC轉換器在SAR組態中的解析度,而每個權值則代表一個二進位元。
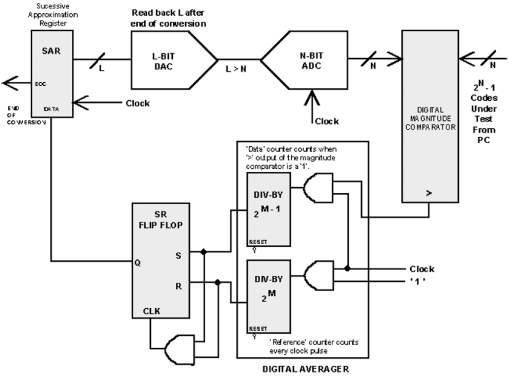
| 《圖七 逐次逼近以及DAC組態可以用來取代類比伺服迴路中的積分電路》 |
|