在許多情況下,量測品質和維持高取樣率下能持續擷取資料的能力有關。在下文將以實例證明,數位器的記憶體深度可決定量測品質及精度。配備深記憶體的高速數位器具有強化時域及頻域量測的能力。以下為以最大數位器取樣率進行長時間資料擷取的應用。
- ●訊號調變分析;
- ●抖動效能特徵化;
- ●脈衝高度量測;
- ●視訊訊號測試。
嚴格來說,量測系統的功率是產品效能特徵化、系統反應分析及缺陷分析的關鍵,搭配較深的記憶體可以改善時域及頻域量測的信賴度及精確度。
時域的益處
當在進行時域分析時,了解所利用的一個既定取樣週期及取樣率所能擷取資料的最大時間是非常重要的。因為資料最終會由示波器轉換到主機電腦中的記憶體儲存、顯示及後續分析,示波器資料傳輸率受限於資料匯流排的頻寬,如PCI。因為通常資料匯流排並沒有足夠的頻寬去保持和高速示波器的全取樣率,所以較深的記憶體是有必要的。藉由較深的記憶體,示波器可在較長的時間內以最大的速率擷取資料,所以其擷取時間區間便隨之增加。擷取時間區間決定了能否擷取整個完整的訊號以作為分析之用。利用以下的公式(S/s=取樣數/秒)可計算擷取時間區間:
或就最大取樣率而論(受限於示波器的規格):
內建擷取記憶體=記錄於示波器內建記憶體的最大取樣數
當選擇取樣率時必須考慮Nyquist理論。該理論說明一個訊號必須以至少二倍以上於其最高頻率成分的取樣率進行擷取,以精確地於示波器上重現其波形。低於其Nyquist頻率的取樣率會導致頻譜區間中的高頻部分失真。所謂失真即因太低的取樣率而導致錯誤的低頻訊號現在擷取的資料當中。(圖一)顯示一個25MHz的正弦波以30MHz取樣頻率的類比數位轉換器擷取所得到的結果。虛線表示25MHz頻率的訊號因為帶通效應,反而被錯誤地表示為一個5MHz的正弦波。為了避免失真,必須以大於50MHz的取樣率來擷取這個25MHz的正弦波。這是說明在訊號量測上維持高取樣率重要性的一個例子。
在上文的公式中,可以以較低的取樣率換取較長的取樣區間,因為示波器內建的記憶體深度是固定的。較深的記憶體在維持高取樣率的情況下可以擷取較長的時間。受限於示波器的記憶體深度,要去擷取封包化的波形是相當困難的,如影像訊號、磁碟讀取頻道及由許多成分組合而成的序列通訊訊號等。通常,唯一的方法可以去擷取整個訊號包絡便是降低取樣率。然而,一個較低的取樣率會造成訊號品質下降及導致訊號包絡中個別的高頻訊號失真。舉例來說,一個NTSC影像訊號包含每秒30張畫面的畫面速率,以及從30Hz到4.2MHz的頻率成分。為了能夠在100Msps的速率下擷取整張畫面,需要一台可以擷取超過3.3MB筆資料的示波器。一台配備1MB記憶體的示波器將減少其取樣率至約30Msps或以下。(圖二)及(圖三)表示在擷取一整張NTSC影像畫面訊號時,減少取樣率從100Msps到20Msps情況下,訊號衰減的結果。注意在水平線的顏色區域有部分訊號資訊已經損失了。
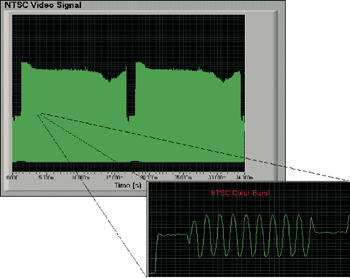
| 《圖二 以100Msps擷取的單張NTSC影像畫面》 |
|
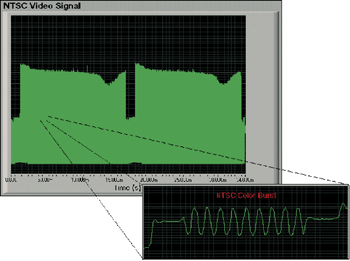
| 《圖三 以20Msps擷取的單張NTSC影像畫面》 |
|
(圖四)則顯示使用深的內建記憶體在一個延伸的時間區間去維持高取樣率的好處。一台具有100Msps取樣率及100KB內建記憶體的示波器可以支撐其最大的取樣率僅維持1個毫秒。為了可以擷取2個毫秒的資料,這台示波器得減少其取樣率至50Msps或甚至以下。一台具有100Msps取樣率及32MB內建記憶體的示波器則可以支撐其最大的取樣率為320個毫秒。
頻域的益處
高速示波器常用於擷取訊號以便於頻域分析。當執行頻域分析時,考慮失真效應是非常重要的。同樣的,Nyquist理論陳述必須以至少二倍於訊號頻率的取樣率去擷取訊號,否則高頻訊號的部分會失真,並且在通帶上反而顯示為較低頻率的訊號。如果取樣率大於二倍擷取訊號的最高頻率,則頻域分析才是有意義的。
頻率解析度
有幾個FFT的演算法用於計算離散傅立葉轉換(DFT)。NI-Scope儀器驅動程式使用劈根實數FFT演算法。這種劈根實數FFT演算法計算n個點,這邊的n是2的指數。如果擷取的點數並非2個指數倍數,則會在波形的尾部補0以增加資料點數至次高2的指數。雖然補0增加了資料點數,但其不影響FFT的結果。對n個點執行FFT運算造成有n/2個點落於正頻域區。這些點定義一個介於DC及取樣率一半間的頻率範圍。一旦點數已知,則可以使用下列公式計算FFT量測的頻率解析度。
依上述公式,當取樣率減少及點數增加時,頻率解析度便會改善。減少取樣率通常是個不討喜的方法以改善解析度,因為其減少了頻率的展延或可用的頻寬。藉由深的內建擷取記憶體,示波器可以在一個長時間內維持一個高取樣率,等同於增加擷取的點數及改善頻率解析度。
舉例來說,使用一台100KB記憶體及最高100Msps取樣率的示波器時,可以從以上公式計算出其頻率解析度。取樣率100Msps及取樣點數設定為100,000點的頻率解析度為762.9Hz,其頻率展開為DC到50MHz。100,000點會補0至131,072點,100Msps除以131,072得到頻率解析度為762.9Hz。
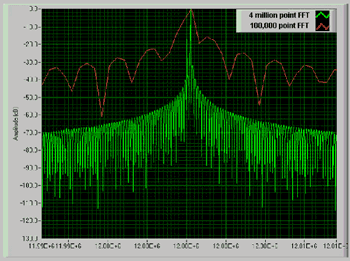
| 《圖五 當擷取400萬個點及10萬個點分別的FFT頻率解析度》 |
|
(圖五)顯示當針對一個擷取的波形進行頻率分析的最佳頻率解析度。在頻率上非常靠近的二個訊號在有限的頻率解析度下會顯示為同一根突峰。在圖五中所擷取的訊號包含12.000000MHz及12.000180MHz的頻率成分。一台記憶體為100KB及最大取樣率100Msps的示波器無法解析這二個頻率。即使降低取樣率至二倍訊號頻寬仍無法讓儀器解析這二個訊號。因此可使用配備深記憶體示波器擷取400萬點去解析這二個突峰。
頻譜洩漏及視窗化
當使用離散傅立葉轉換(DFT)或FFT去了解訊號的頻率內容,這是假設已經擷取了一段週期性重覆的波形。因為FFT會試著藉由複製有限的擷取點數去近似連續傅立葉轉換(CFT)。如果擷取的資料並不包含一個整數週期,則無限區間中會有數個不連續點在有限擷取點的連接處。(圖六)顯示擷取非整數倍數週期的效應。
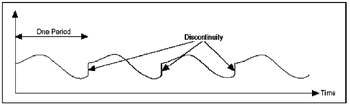
| 《圖六 以非整數週期複製一個有限擷取所造成的不連續點》 |
|
這些人工的不連續點在FFT的頻譜上為原始訊號中沒有顯現的高頻成分。這些頻率可能高出Nyquist頻率許多,並且失真頻率落於0及fs/2之間,這裏的fs是指取樣率。利用FFT所得到的頻譜並不是原始訊號真實的頻譜,而是一個失真的頻譜。這顯示在某一頻率上的能量洩漏至另一頻率上。這個現象稱為頻譜洩漏。頻譜洩漏造成細長的頻譜線展延成較寬的訊號。
(圖七)顯示一個由示波器所擷取的正弦波,及其對應的FFT強度(以分貝計量)。這個時域波形有一個整數週期(以此範例為2), 所以是假設這個週期並不會造成不連續點。
(圖八)是一個非整數倍時域波形頻譜。這個訊號的週期延伸造成類似於(圖六)中週期延伸的不連續點。注意能量是如何展延至一個較寬的頻帶中,所以介於FFT尖峰及鄰近區域間的高度因而衰減了。這種由於能量的洩漏所造成的頻譜失真稱為頻譜洩漏。頻譜洩漏扭曲了能量由一個特定頻率展延至鄰近頻帶的量測結果。
擷取訊號因非整數週期連接點處所造成的不連續點,而造成頻譜洩漏的存在。此時可以利用名為視窗化的技術來減小這種因非整數週期的FFT運算所產生的效應。視窗化在每一個有限區間內減小在邊界上不連續點的強度。
視窗化包含將波形乘上一段有限長度的視窗區間,而這個區間的振幅緩慢地變化至二端為0。因此當針對一段有限長度的資料執行FFT頻譜分析時,可以使用視窗化技巧減小轉換邊緣的振幅改變,因此可以在無限區間內消除不連續點。通常有六種視窗化的種類可以選擇,包含rectangular、Hanning、Hamming、Blackman、triangle及flat top。
(圖九)顯示當擷取一個非整數週期的訊號時,使用Hanning視窗化所帶來的好處。第一張是從圖八所擷取到的原始訊號,第二張圖顯示在經Hanning視窗化後的時域訊號,第三張圖為經Hanning視窗化後訊號的FFT?頻譜圖。注意圖九中經視窗化FFT和圖八未經視窗化FFT的訊號相比,其頻譜洩漏已下降許多。
如果欲觀察的波形包含二個或以上的訊號,且這些訊號在頻域上僅只有些微的差異,則頻譜解析度益顯重要。在這個情況下,最好是選擇一個主要波瓣較窄的視窗,如Hanning視窗。在既定的頻率區間中,如果單一頻率成分的強度、精度較其精確的位置來得重要,則選擇一個波瓣較寬的視窗,如flat top視窗。Hanning是最常使用的一種視窗,因為它提供較佳的頻率解析度且可減少頻譜洩漏。然而,考慮配備較深的記憶體以提升頻率析度,flat top視窗反而提供比Hanning更多的好處。因為flat top視窗提供最佳的振幅精度及最陡峭的邊緣波瓣。
動態範圍
當進行頻率量測時,了解其動態範圍是相形重要的。所謂動態範圍即量測系統所能處理的最高準位對最低準位的比值。此處解釋在較大振幅訊號存在的情況下所能量取的最小訊號振幅有多少。
類比數位轉換器(ADC)的內部缺陷限制數位示波器的動態範圍。在類比前端及ADC的非線性反應造成共振扭曲,並且在FFT的頻譜分析上顯示為錯誤的訊號。
(圖十)顯示一個10MHz訊號的FFT頻譜。注意出現在圖上額外的頻譜線並非原始10MHz訊號的任何部分。介於基本10MHz訊號及在30MHz最大失真頻譜的動態範圍約是46dB。
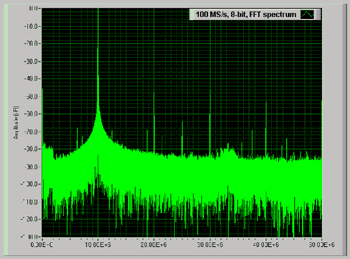
| 《圖十 以100Msps擷取位於10MHz的FFT頻譜圖》 |
|
增加用以計算FFT頻譜的取樣數可以減少非同步的雜訊底線。每一個FFT頻帶顯示在頻帶中所有的能量。增加更多的FFT取樣數反而使每個頻帶的寬度變狹窄了。窄化每個頻帶的寬度會降低每個頻帶的所有雜訊,並且降低雜訊底線。這種雜訊底線的改善是被證實的,因為增加FFT計算的點數並不會改變整個FFT頻譜的所有能量。(圖十一)顯示增加擷取的點數從1024點至400萬點的效應。
增加取樣點數減少來自於非同步雜訊源的雜訊底線,並且顯示額外頻譜線的發現是由於示波器內部的缺陷所造成。某些示波器包含有效位元數(ENOB)或訊號對雜訊比(SNR)等規格。所謂SNR即是所有訊號的功率對雜訊功率的比值,常以分貝作為單位。SNR及ENOB能以下列公式計算求得。
平均化
可以針對示波器所擷取到的資料執行二種型態的平均化。時域平均化,也稱為波形平均化,是在計算FFT前對時域的訊號作運算。而FFT平均化,相反地,是藉由擷取每個波形,分別計算FFT,然後對FFT頻譜取其平均。每種平均的類型各有益處。
時域平均化是藉由針對多個觸發點所得到的資料點取平均。這將衰減示波器的內部效應,如非同步雜訊效應,因此可以增加動態範圍。雜訊底線也依平均化的點數減低至一定的程度,但雜訊底線的變異仍維持一個定值。這些效應如(圖十二)所示,顯示針對所擷取的訊號其動態範圍取波形平均的益處。
FFT平均化是藉由擷取個別波形,分別計算FFT,然後對FFT頻譜取平均。這個種類的平均化對減低雜訊底線的變異是非常有效的。(圖十三)顯示FFT平均化的效應。
|
|
 |
PAC可提供工程師高級控制所需要的PC功能、即時分析或企業連接能力,同時保有PLC的可靠性。相關介紹請見「PAC進軍自動化領域優勢概論」一文。 |
 |
資料記錄是相當普及的量測應用,在多種領域中皆可見其身影。資料記錄可讓工程師測量不同的現象,從天氣到工廠效能。你可在「PC-Based資料記錄技術發展與現況」一文中得到進一步的介紹。 |
 |
電信研究所已針對ATM高速網路進行關鍵組件之開發,目前已完成寬頻虛擬路徑交換機(BEX-VPX)、寬頻數位器(BEX-AMX) 、ATM LAN SWITCH/HUB等之發展。在「中華民國國家資訊基礎建設之遠景與藍圖」一文為你做了相關的評析。 |
|
|
 |