當筆者開始撰寫本文時,有人看見標題便問:「您沒有小孩,對吧?」雖然過去的確有管過小孩的經驗,但一般人在其一生中都忘記了這兩件事:極度的愉快及痛苦。而這也是為什麼人類一直持續往回走的原因。本文不是要回憶到像是處理雜訊電路那樣痛苦的經驗。主要是關於如何愉快地在數位領域中處理這些困難的類比式噪音。
解決類比到數位的轉換
在混和式信號線路的完美轉換是:轉換器每次都會產生一個重複、精確的數位式結果。使用噪音降低技術,像是使用具備精密架構的類比式濾波器來降低噪音並用於移除不想要的信號。不過,另一種解決類比到數位轉換問題的方式是「設計」噪音到信號中以取代掉。例如,如果致力於在電路上使用低噪音策略,可由一個12位元轉換器獲得12位元的精確性。作為另一種方式,可容許一定程度的白噪音進到電路中,接著使用一個處理器或控制器數位濾波器來轉換。在這個場景中,電路便能夠產生14、15或甚至16位元的精確性。如果在電路中具有噪音,可藉由使用超取樣技術以在數位濾波器的輸出上達到較佳的解析度。
例如,若使用取樣移動式平均數位濾波器,便可使用下列公式來計算所要增加到轉換解析度上的位元數(
N)。如果想將解析度由11位元增加到14位元,便需要累積並平均到64個取樣資料。對於增加解析度而言時間是最主要的問題。移動式平均數位濾波器邏輯法則累積幾個取樣以能夠計算最終的結果。而這些取樣的累積需要時間。有限脈衝響應(FIR)和無限脈衝響應(IIR)數位濾波器也非常適用於這個工作。
如果時間充裕,這聽起來像是一個簡單的解決方案。不過,在開始使用這個類比與數位系統組合電路之前,有一個問題應先考量。必須知道ADC數位輸出隨時間所產生的情況。當檢視數位碼隨時間變化時,長方條式的描跡是一種最適當的工具。在這個圖中會顯示每一個碼發生的數量。例如,在(圖一)中的長條統計圖顯示來自一個12位元(取樣率=20ksps)ADC的1024個重複資料樣本。
結論
如果想要在轉換器上成功地增加解析度,便需要確保來自ADC的噪音在本質上是屬於高斯。在一各長方條狀圖中,高斯噪音看起來像是在一個中心碼上的統計式常態分佈。在圖一中的資料並未追隨一個常態分佈的形狀。事實上圖一的形狀看起來像是一個雙峰響應。除此之外,該系統的輸出平均應該是2236而非2297。所以一個數位濾波器不會「修復」這個資料。本系統的噪音來自於一個LED陣列。一個較差的陣列設計所產生的高電流雜訊會使得噪音在電路板上造成無法容忍的干擾。
若設計人員在ADC的輸出上使用一個數位濾波器,這並非意味著已免除了所產生的是何種資料的責任。數位濾波器可改進類比到數位的轉換,但是這只在非常有信心對於資料的噪音響應在本質上是高斯時才有效。
(作者任職於Microchip Technology)
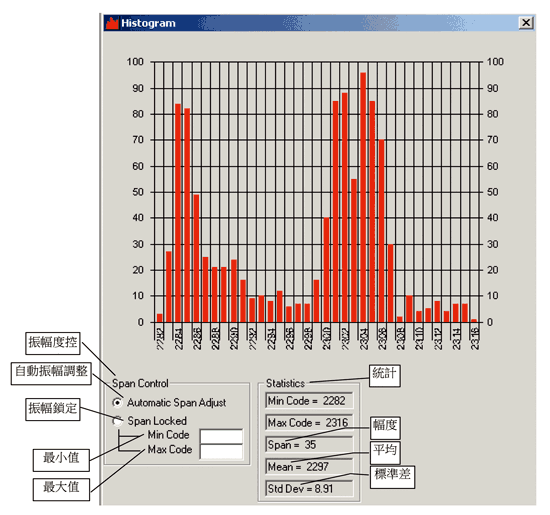
| 《圖一 這個長條圖顯示來自ADC的資料是雙峰形。這是困難去使用數位濾波器的原因,困難點在精確地將一個數位碼實際回復成它所代表的類比電壓輸入。》 |
|