要了解相位雜訊對取樣時脈的影響,可重新檢視取樣操作的數學。輸入訊號,x(t)與一串完美的脈衝相乘表示理想的取樣操作。此流程產生一個取樣數值的串流,y(nT),如(公式一)所示。
在數學運算裡,時域上的相乘與頻域上的卷積為一體兩面。然而,時域上理想的脈衝串可轉換為頻域上的脈衝串。頻譜上的訊號進行卷積會造成相似的週期性數位訊號頻譜。
實際上,取樣波形既非完美的脈衝,在時間上也不穩定。比較實際的做法是在某個非常短的時間窗內,將最後的取樣電壓當作輸入訊號進行加權平均。然而,由於關心時脈抖動的影響,因此將繼續使用脈衝作為取樣波形,但包含了抖動項。如果時脈抖動的效應有列入考慮,則脈衝函數的衰減項中會包含隨機成分τj。一般而言,τj會以具有平均值為零與標準差為σj的高斯(Gaussian)隨機過程來建立模型。取樣的訊號現在變為(公式二)。
如(公式二)顯示輸入訊號是被抖動取樣函數所展開。基本上,項會造成微小、殘留的頻譜偏移(調變)因而將訊號頻帶展寬。(圖一)顯示了此效應。
這裡採用兩個步驟來描述(公式二)所顯示的效應。抖動項會將原始的訊號頻譜進行調變,如(圖一)(a)所示(包含取樣時脈)。圖一(c)顯示在亞奈取樣之後的數位、抖動-調變的頻譜。抖動對訊號頻帶有兩個影響。首先,抖動所造成殘留的展頻(由於相近的同相位雜訊,如圖五(b))直接對頻帶內的SNR造成劣化。其次,亞奈取樣造成頻帶外的雜訊,而混疊在訊號頻帶中,因此更增加雜訊背景值。
在圖五(c)中,「跨過」π倍數(標為垂直的虛線)頻率邊界的頻帶外雜訊,會反折回訊號頻帶。如果此頻帶外雜訊夠高,會嚴重提高雜訊背景值。這些複合效應強調相近的同相位雜訊與距離時脈頻率很大偏移處的相位雜訊之重要性。此效應可以藉由增加取樣頻率來作某種程度的消除,但這也會造成影像在頻率上展得更寬,而且要對需要處理的取樣數量增加進行取捨。然而在某些應用上,這仍是一種可接受的取捨。此範例也強調訊號路徑中的濾波限制在ADC輸入端頻道外雜訊之重要性。
下一部分會檢視如何結合數個雜訊來源的效應表示為時脈抖動的公式,以了解不同來源的影響並且定義一個時脈抖動上限。此範例會結合熱雜訊、量化雜訊與取樣時脈相位雜訊。如果假設各雜訊來源彼此是獨立且不相關的(合理的假設),則複合的SNR可以表示為(公式三)。
雖然常認知的SNR是在對數單位下所表示,但注意上式的每項都是以線性單位表示的數值。在公式一中使用變異數的表示法來強調處理隨機過程,它甚至可以包含所需的訊號。
為了找出各雜訊源的SNR,從熱雜訊開始。出現在特定的固定頻寬Δf中的熱雜訊功率為雜訊密度乘上Δf:Pth-noise=N0×f=σ2T,其中N0=雜訊頻譜密度,單位為W/Hz。
要在ADC輸入端設定數值N0需要設計師進行一個端點到端點的訊號路徑分析以找出系統雜訊指數。參考公式三,各個次系統(接收器、訊號分配放大器、分歧器、與電纜線)具有相對應的增益與雜訊指數,整合以上獲得如(公式四)所示的最後的系統雜訊指數[1]。
其中下標表示路徑中相連接的次系統(或元件),而參數Fn與Gn為分析中所包含各個次系統或元件的線性數值雜訊指數與增益。
如果在訊號路徑上有數個元件,設計看起來就可能相當複雜。但有一個拯救的方法是,路徑中第一個元件會主導最後的系統雜訊指數。注意相連接的次系統或元件都列入計算中,其對雜訊指數的貢獻與其和上傳串流次系統增益乘積成反比,也就是說,各下傳串流次系統或元件對整體雜訊指數具有快速削減的效應。有經驗的系統設計師了解此點,因此路徑中第一個元件通常是低雜訊放大器,基本上它會將系統雜訊指數設定在很低的數值。因此,如果有非常大量來自ADC的訊號路徑上傳串流,可藉由只觀察路徑中前面幾個次系統或元件,就可獲得系統雜訊指數良好的合理估計。一旦可估算NFsys數值,就可使用(公式五)來找出ADC輸入端的雜訊功率頻譜密度,其單位為dBm/ Hz。
此功率頻譜密度相當重要的因素有二。首先,具有很大輸入頻寬的ADC可能導致動態範圍損失,因為雜訊功率(σ2T)正比於頻寬。其次,雖然基頻的處理通常包含濾波器的步驟,以消除未落在所需頻帶內的雜訊,但殘留的頻帶內雜訊對整體SNR計算也會有貢獻。在對數單位中,雜訊功率為頻譜密度對數加上所考量的頻寬,取其10log的值。
要找出在所需頻帶中的雜訊功率(單位為dBm),取代訊號頻寬為ΔfBW。
如果單位為dBm,訊號功率已知,可扣除雜訊功率以獲得單位為Db的SNR值,並將之轉換為線性數值。或者可以將雜訊功率轉換為等效的RMS電壓,並將SNR以RMS電壓來表示。
本範例中第二個雜訊源為量化雜訊。ADC解析度限制會引入量化雜訊,如(圖二)所示。圖中顯示一般平移二元量化器的轉換函數,水平軸表示量化器的輸入電壓範圍,分為1LSB的固定間隔,各輸入電壓取樣值對應到這些區間中的一個。
基本上,量化器將取樣的電壓數值以無條件捨去法截取出量化區間中最接近的整數值。在圖二中,任何Vin=V(nTs)落在區間[7Δ/2、9Δ/2]的數值會對應到數位數值0100。如果將此數位數值轉換回電壓時,可能會指定一個7Δ/2=(7/2)×(Vref/2N)的數值。實際上,真實的電壓數值將更大,因此量化器會引入誤差電壓Ve。此誤差項(量化雜訊)可視為真實訊號數值的外加雜訊。因為任何組合的輸入電壓數值落在特定量化區間之分佈密度是均勻的,因此誤差項的分佈密度項(或稱為量化雜訊)也是均勻的。量化雜訊功率為此誤差項的變異數,即:
要找出關於此ADC輸入端量化雜訊功率,將之除以輸入電阻R。最後,將之除以Fs/2,可算出量化雜訊功率頻譜密度:
在將此項轉換為對數單位dBm之後,如同熱雜訊一樣,可計算出頻帶內的量化雜訊功率,並使用功率值或RMS電壓值來計算出SNR。注意此量化雜訊功率頻譜密度與ADC解析度(N)和取樣頻率(FS)有反比的關係。因此,如果以RMS電壓項來表示SNR,可研究不同的解析度與取樣頻率對SNR的影響。
如果取樣時脈沒有抖動,則訊號頻帶中(頻帶內)的雜訊功率頻譜密度會是熱雜訊與量化雜訊的和(在此範例中)。在此情況下,最底線的SNR為:
在(公式十二)中,設計師可以使用這些SNR項來合成不同的參數效應,例如取樣頻率與ADC解析度。可以研究這些參數的影響,以定義出符合目標SNR(或ENOB)的邊界值。在完成這樣的工作並嘗試選擇N與FS的數值之後,可以引入由於取樣時脈抖動所造成的SNR劣化。在本文的第一部分中顯示由於取樣時脈抖動造成的SNR為:
很重要的是要,記住在此公式中σj實際上是時脈RMS抖動加上ADC的RMS孔徑抖動方和根(root-sum-square)值。針對由於抖動造成SNR使用(公式十三),並將之與公式三與公式十二結合,可以建立形成底限SNR的抖動與SNR劣化裕度的參數。
在(公式十四)中,x為總SNR中由於抖動造成特定可接受的劣化值(單位為dB),fsig為所使用訊號的最高頻率,以及上述其他參數。可以根據不等式來設定抖動上限。或者,只要針對特定應用定義一個目標(最小可接受的)SNR,並且使用修正的公式十四。
以WCDMA系統為例,其訊號中心頻率為245MHz、頻寬為5MHz、操作在61.44MSPS的取樣頻率。自動增益控制電路放在ADC前面,設定用來對訊號功率作平均,在ADC輸入端產生-10dB的全刻度(dBFS)訊號。ADC輸入範圍為1Vp-p,且ADC輸入端在5MHz頻寬中的熱雜訊功率設定為-90dBm。如(圖三)顯示三種不同的ADC解析度:8、10、與12位元的圖形。在三種情況中,以量化雜訊設定雜訊背景值。各個情況中,曲線顯示當抖動增加時,SNR會劣化。對於12位元ADC而言,即使當SNR從72dB劣化到59dB,最大的抖動限制仍可維持在低於1皮秒。
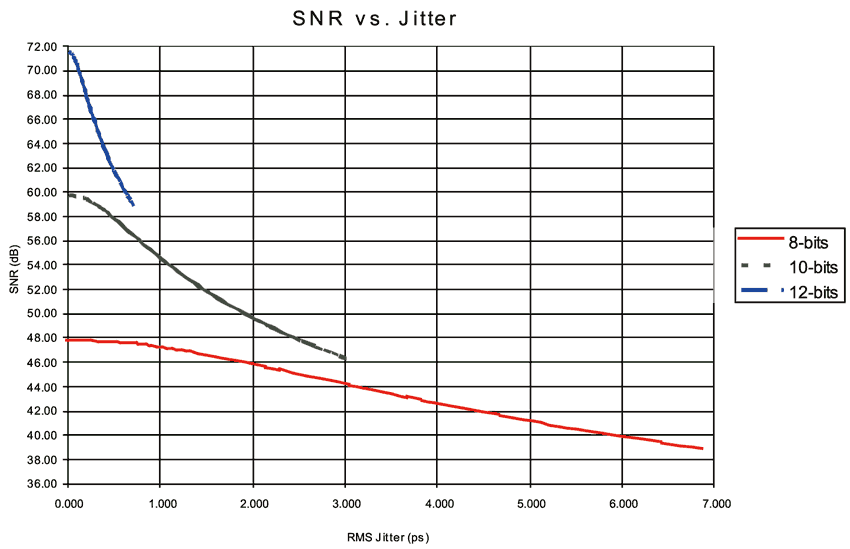
| 《圖三 抖動與SNR關係圖》 - BigPic:849x548 |
|
結論
本文討論在使用帶通取樣來實現高效能多頻道、數位接收器架構時,系統設計上所面臨的挑戰。對於ADC而言,要有非常高的輸入頻寬與高取樣頻率。本文中強調系統觀點的設計,亦即設計選擇,例如ADC速度與解析度,以及取樣時脈需求,可由來自ADC界面上傳串流來定義系統特性。在系統的前端選擇適當的低雜訊放大器(LNA),對整體雜訊指數具有重大的影響,也會影響設定ADC輸入端的雜訊密度。
此外,低雜訊取樣時脈的產生與分配也會主導系統的效能。由於抖動造成的取樣雜訊影響整體SNR,因此必須一起評估所有其他雜訊源造成的影響,例如熱雜訊與量化雜訊,以達成所需頻帶內SNR的取樣時脈效能。
---作者任職於NS美國國家半導體介面部門---
<參考資料:
[1] T. T. Ha,數位 衛星 通訊,2nd Edition,McGraw-Hill,New York,1990.
[2] M. E. Waltari, K. A. I. Halonen,低電壓與高速度A/D轉換器電路技術,Kluwer Academic Publishers,Boston,2002.>