傳統上設計毫米波電路,通常是使用SiGe BiCMOS或Ⅲ-Ⅴ族化合物半導體來實現。但由於CMOS製程快速的進步,以及低成本、高電路整合的優點,使得CMOS毫米波電路設計受到矚目。雖然CMOS電晶體的基底具較高的耗損性,以及電感的品質因子甚低,CMOS半導體技術仍然擁有製作微波及毫米波積體電路的潛力。鎖相迴路以及頻率合成器廣泛地應用在現代的無線通訊系統中,然而壓控振盪器以及除頻器的效能,限制了它們的最高操作頻率。因此,一個可以操作在高頻的除頻器,將是設計CMOS高速鎖相迴路的挑戰之一。除頻器的設計,主要可以分成兩大類:數位型態和類比型態。數位型態的除頻器,主要是以D型正反器(D flip-flop)的方式實現。它們的優點是操作頻寬較寬、多變的除數以及較小的面積,但速度與功率消耗是主要的缺點。類比的實現方式主要包含:注入鎖定式(injection-locked)以及米勒(Miller)除頻器。雖然具有狹窄鎖定範圍的缺點,但是基於高速操作以及低功率消耗的考量,類比式除頻器仍然是毫米波頻段的熱門首選。
除頻器的種類
數位式除頻器
在操作頻率較低時,最常使用的除頻器是以D型正反器為基礎,所構成的除頻器電路。採用一個D型正反器以及一個反向器串接,可以實現一個除二的除頻器。欲實現多變的除數,可使用計數器的方式。圖一是一個可以產生50%工作週期(duty-cycle)的除三除頻器[1],電路由三個位準觸發(level triggered)D型正反器所建構。
類比式米勒除頻器
米勒除頻器是前述實現類比式除頻器的方法之一。利用混頻器IF輸出端串接帶通濾波器,然後回授到LO端形成迴路,達到除二的效果[2],如圖二所示。基於這個理論,電路如果採用N階諧波混頻器(Nth harmonic mixer),則可得到除N+1的除數。但是階數越高的混頻器,需要消耗更多的功率以提供足夠的混頻器轉換增益,來避免電路無法鎖定。
類比式注入鎖定式除頻器
高操作頻率以及低功率消耗是注入式鎖定除頻器的最大特點。主要有兩類實現的方式:環形振盪器以及共振腔式的除頻器。圖三是一個以環形振盪器電路為基礎的除三除頻器[3]。輸入訊號經由電流源的汲極端,從三級反向器的共源極點注入,將輸出訊號鎖定在1/3的輸入頻率。圖四是準差動注入鎖定除二除頻器[4],電路也是以環形振盪器電路為基礎。傳統的作法是將輸入電晶體串聯在其中一級的反向器下方,使得供應電壓在設計上無法降低。然而[4]將輸入電晶體置於兩級反向器的輸出點之間,以降低整體的功率消耗。圖五是一個注入鎖定除頻器[5],注入訊號經由M3,傳遞到交錯耦合差動對的共源極端。由於共源極端的訊號頻率會是輸出頻率的兩倍,因此藉由影響這個兩倍頻的訊號,達到除二的效果。另外一種共振腔式注入鎖定除頻器,如圖六,為一個直接注入鎖定除頻器[6]。電路的原型是一個電容電感式振盪器,在差動輸出端之間加入一個開關,用來調制差動輸出訊號,達到除二的功能。表一比較了不同型態除頻器的效能參數。由前述,基於高速操作以及低功率消耗的考量,類比式除頻器仍然是毫米波頻段的熱門首選。
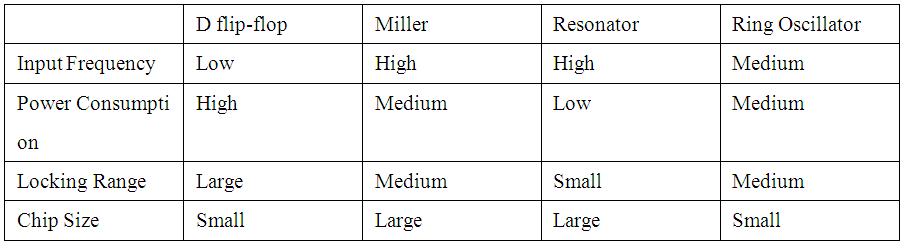
| 《表一 不同型態除頻器的效能參數。》 - BigPic:903x250 |
|
CMOS毫米波除頻器
寬頻除頻器
圖七是一個具有寬頻操作的直接注入鎖定除頻器電路架構圖[7]。電路採用電容電感式交錯耦合差動對壓控振盪器作為除頻器的基本架構,產生的自振頻率為fout。電晶體M1及M2用來產生負阻抗以抵銷電容電感的耗損。另外,為了增加最大可操作頻寬,電路採用了電晶體變容器當作微調以及跳頻電容當做粗調。電晶體M3是除頻器電路的核心,用來當作開關。當M3斷路時,電路的輸出頻率是壓控振盪器的自振頻率。當開關導通時,電路的差動輸出訊號被強迫短路。以此類推,輸出訊號在一個週期內將被會短路兩次,因此電路可以達到除二的效果。鎖定的概念如圖八所示。
電路使用TSMC 0.18μm 1P6M CMOS製程研製,面積為0.81mm×0.54mm。在1伏特的供應電壓下,電路消耗功率是8毫瓦。除頻器在沒有使用變容器以及跳頻電容時,量測到的鎖定範圍是2.6GHz。在低頻帶的情況下,除頻器操作範圍可從43.2GHz到47.3GHz,而在高頻帶的狀況下為44.2GHz到49.1GHz。因此在輸入功率為0dBm時,電路的最大操作頻寬從43.2GHz到49.1GHz。然而在輸入功率降低為-10dBm時,電路仍可操作在43.8GHz到48.8GHz的範圍內。圖九是除頻器量測的input sensitivity。
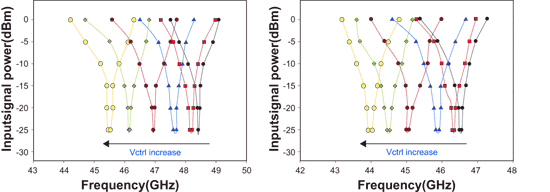
| 《圖九 除頻器的input sensitivity。(左)高頻帶,及(右)低頻帶。》 |
|
除三除頻器
類比式直接注入鎖定除頻器的特色是高操作頻率以及低功率消耗。但是它們通常有除偶數的限制[8]。然而在通訊系統中,需要一個除三除頻器來避免LO訊號對接收端以及發送端的干擾[9]。如果使用環形振盪器除頻器,操作頻率會受到限制。使用高次諧波混頻,將使功率消耗變大。圖十是一個結合米勒除頻器以及直接注入鎖定除頻器的除三除頻器[10]。圖中左邊是一個Double-balanced Gilbert cell混頻器,右邊是一個互補式直接注入鎖定除頻器,而輸入訊號從混波器的RF端潰入。注入鎖定除頻器的差動輸出直接回授到到混波器的LO端,IF的差動輸出訊號可以用來控制互補式開關M1及M2,當作注入鎖定除頻器的輸入訊號。除三除頻器的操作原理建構在混頻器的混頻以及除二除頻器之上。假設輸出訊號的頻率是fout,與輸入訊號混頻,產生fin+fout和fin-fout兩種頻率。由於混頻器的負載設計在2fout以及除二除頻器本身具有濾波的功能,fin+fout將會被濾除。所以當除頻器鎖定的時候,輸出訊號fout=1/3fin。由這個小型系統的架構,可以延伸成一個可除奇數的除頻器,如圖十一所示。在傳統米勒除頻器的迴路中,插入一個除2N的除頻器。經由適當的設計以及計算,可以得到除(2N+1)的除頻器。
除三除頻器使用TSMC 0.13μm 1P6M CMOS製程研製,晶片面積為0.8mm×0.6mm。在2伏特的供應電壓之下,電路共消耗16毫瓦的功率。量測到的鎖頻範圍,再0dBm的輸入功率下是100MHz。圖十二為除三除頻器的input sensitivity。
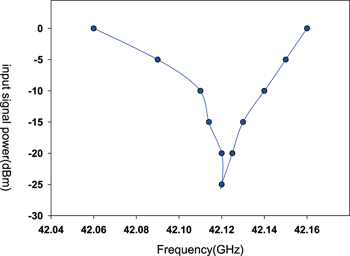
| 《圖十二 除三除頻器的input sensitivity。》 |
|
直接除四除頻器
一般來說,除四除頻器通常採用串聯兩級除二的架構[2],或利用高階諧波混頻的方式來實現。兩級架構需要分開設計且消耗額外的功率。而高階諧波式除頻器需要消耗大量的功率以增加混頻器的轉換增益。因此,本電路採用新的直接除四的架構,降低總功率消耗。電路的方塊圖如圖十三所示[11],包含混頻器、除二除頻器以及雙推式(push-push)倍頻器。假設電路的輸出頻率為fout,經過雙推式倍頻器,產生頻率為2fout的訊號,之後潰入混頻器的LO端。經過混頻後,IF輸出端主要會有fin-2fout以及fin+2fout的成分。因為注入鎖定除頻器固有的濾波效果,使得fin+2fout訊號被濾除。經過計算之後,fin=4fout。使用TSMC 1P6M 0.18μm CMOS製程研製的除四除頻器如圖十四所示。電路架構採用互補式交錯耦合差動對的壓控振盪器,降低電路自振所必須消耗的功率,自振頻率為fout。N+ N-well電晶體變容器用來調整除頻器的自振頻率。在NMOS以及PMOS耦合差動對的源極端,分別串聯一段長度為自振頻率波長八分之一的傳輸線,以提供直流路徑到供應電壓源和接地端,同時在輸出二階諧波頻率時,產生高阻抗。將兩端點分別連接到高頻混波器的LO及IF端,當LO與輸入訊號產生混頻的效果,在除頻器鎖定的時候,LO及IF端訊號的頻率將會是輸入頻率的一半。之後再經過注入除二除頻器[5],而達到除四的效果。
除四除頻器電路使用0.77mm×0.8mm的晶片面積。電路的供應電壓是1.2伏特,共消耗1.8毫瓦。在變容器的控制電壓為0伏特之下,除頻器的自振頻率是10.55GHz,且量測到的鎖頻範圍是200MHz。電路的最大操作頻寬可以從41.9GHz到44GHz。量測的input sensitivity如圖十五所示。
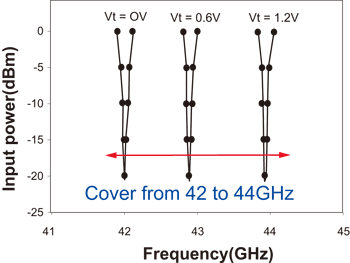
| 《圖十五 除四除頻器的input sensitivity。》 |
|
結論
隨著CMOS製程的演進,通道長度持續縮短,SiGe BiCMOS或Ⅲ-Ⅴ族化合物半導體,主宰毫米波電路的市場,因為CMOS的低成本以及高電路整合的優點,逐漸失去優勢。除頻器廣泛地被使用在鎖相迴路、頻率合成器或通訊系統中。除頻器有許多種設計的方法,各有優缺點。本文概略性的敘述了多種形式的除頻器技術,包含數位式的正反器,類比式的米勒、環形振盪器以及共振腔注入鎖定等。然而毫米波頻段的電路在設計時,需要考量到操作速度以及功率消耗的因素,所以文中舉出三個使用類比式除頻器電路的實作例子。並且提出了改善傳統架構高功率消耗以及除數固定的方法,證實了CMOS半導體技術仍擁有製作微波及毫米波積體電路的潛力。
參考文獻
[1] R. Magoon and A. Molnar, “RF Local Oscillator Path for GSM Direct Conversion Transceiver with True 50% Duty Cycle Divide by Three and Active Third Harmonic Cancellation,” in IEEE RFIC Symp. Dig., pp. 23-26, June, 2002.
[2] Jri Lee and Behzad Razavi, “A 40-Ghz Frequency divider in 0.18-μm CMOS Technology,” in IEEE Symp. VLSI Circuits Dig. Tech. Papers, pp. 259-262, June, 2003.
[3] W.-Z Chen and C.-L Kuo, “18GHz and 7GHz Superharmonic Injection-Locked Frequency Divider in 0.25mm CMOS Technology,” in Proc. European Soild-State Circuits Conf., pp.89-92, 2002.
[4] K. Yamamoto, and M. Fujishima, “A 44-μW 4.3-GHz Injection-Locked Frequency Divider With 2.3-GHz Locking Range,” IEEE Journal of Solid-State Circuits, vol. 40, no. 3, pp. 671-677, March 2005.
[5] H. R. Rategh and T. H. Lee, “Superharmonic Injection-Locked Frequency Dividers,” IEEE Journal of Solid-State Circuits, Vol. 34, pp. 813-821, June 1999.
[6] Ken Yamamoto and Minoru Fujishima, “55GHz CMOS Frequency Divider with 3.2GHs Locking Range,” in Proc. 30th European Soild-State Circuits Conf. 2004, pp. 135-138, Sep., 2004.
[7] Yi-Jan Emery Chen, Shuen-Yin Bai, Tang-Nian Luo, Yueh-Hua Yu, Deukhyoun Heo, “A wide operation range CMOS frequency divider for 60GHz dual-conversion receiver,” IEEE RFIC Symposium Tech. Digest, June, 2006.
[8] K. Yamamoto and M. Fujishima, “70GHz CMOS Harmonic Injection-Locked Divider,” IEEE ISSCC Dig. Tech. Paper, pp. 600-601, Feb., 2006.
[9] R. Magoon and A. Molnar, “RF Local Oscillator Path for GSM Direct Conversion Transceiver with True 50% Duty Cycle Divide by Three and Active Third Harmonic Cancellation,” in IEEE RFIC Symp. Dig., 2002, pp. 23-26.
[10] Tang-Nian Luo, Shuen-Yin Bai and Yi-Jan Emery Chen, “A 43GHz 0.13m CMOS Prescaler,” accepted for presentation at IEEE RWS, Jan. 2008.
[11] Tang-Nian Luo and Yi-Jan Emery Chen, “A 44 GHz 0.18μm CMOS Superharmonic Frequency Divider,” IEEE MTT-S IMS, June 2007.
…作者羅棠年先生為國立台灣大學電子工程研究所博士班學生。
陳怡然先生為美國喬治亞理工學院電機工程博士,現任國立台灣大學電子工程研究所助理教授…