抖動放大電路設計架構 [7] [8]
週期對週期抖動量即為後一個週期邊緣En+1和前一個週期邊緣En之相位誤差,因此若要實現抖動量放大就必需將En和En+1間之邊緣時間差拉大。在本文中將採用電流對負載充放電之原理來達到抖動放大之功能。我們以圖九來說明其操作原理。
抖動放大電路基本上是由兩組不同電流量之電荷幫浦(Charge Pump;CP)與決策電路(Decision Circuit;DC)所組成,而分別由待測訊號SUT、一個週期延遲後之訊號SUTd與兩者之組合來控制。其最基本的想法為利用不同充電斜率(即充電速度)搭配訊號不同起始點(即轉態邊緣)之特性,來合成出具有較大抖動量的時脈邊緣。而為了清楚解釋其放大原理,我們將SUT(S)與SUTd((Sd)依相位關係區分成四個區間,然後分別探討在不同區間內的操作情形。如表一所示。
(表一) 電荷幫浦操作狀態表
|
S Sd |
狀態 |
I |
0 0 |
S1、S2、S3 turn off →
f1=0xI、f2=0xI。 |
|
II |
1 0 |
S1、S2 turn on;S3 turn off →
f1=I+nxI、f2=0xI。 |
- f1以(n+1)xI之斜率往高電位VH移動
- f2仍處於低電位
|
III |
1 1 |
S1 turn off;S2、S3 turn on →
f1=I、f2=I。 |
- f1之速率改變為I但繼續往VH移動
- f2也以I之速率開始往高電位VH移動
|
IV |
0 1 |
S1、S2 turn off;S3 turn on →
f1=0xI、f2=I。 |
- SUT訊號之負緣產生(tf)
- f1將從高電位VH回歸低電位VL
|
搭配圖九與表一之敘述,從中可以得知在初始狀態時因SUT與SUTd為低電位,開關皆turn off,所以並無任何電流對負載做充電因此輸出結果(1、2)將為低電位(VL)。但若當兩個phase間有抖動存在時,SUT會為高電位而SUTd為低電位。此時1會以(n+1)倍的電流對負載充電pull up,而2因S3 turn off所以將保持前一狀態的低電位。接著經過Δτ的時間後,SUTd也pull high,促使S3 turn on、S1 turn off,此時1和2將一起以I的速度往高電位移動。但是仔細觀察Region II和Region III之過程,因在Δτ的這段時間裡1先以較快的速度啟動,若Region III在相同充電的斜率條件下(電流量皆為I)其會先到達穩態位準;而接著再經過n*Δτ時間後,2才也會到達此位準。此時從圖九中可以看出1、2與所設定的臨界電壓(Vth)有兩個交點,若用兩組決策電路將轉態點判斷出來即可產生兩組不同相位差的輸出訊號(Out1、Out2)。所以利用上述之條件,我們可以簡單以公式一來表示出輸出與輸入間的關係:
其中OUT為Out1、Out2間的相位差(放大後之週期對週期抖動量)、IN為SUT、SUTd間的相位差(放大前之週期對週期抖動量),而A即代表放大倍率。
利用上述概念,本創作即可將時脈訊號之週期對週期抖動量加以放大,來彌補時間-數位轉換電路的不足。然而單純光靠電流充電能力的行為模式來達成放大目的,會面臨電路操作瓶頸進而導致測試誤差產生,例如放大倍率的非線性或是操作頻率變化等,接下來我們會針對這些效應提出解決之道。
抖動放大電路及Pulse Remover設計的分析
(表二) 符號表示
VH |
充電之最高位準(即高穩態點) |
VL |
充電之最低位準(即低穩態點) |
ts1 |
1到達高穩態點之時間 |
ts2 |
2到達高穩態點之時間 |
tf |
負轉態邊緣 |
Vth |
臨界電壓 |
在抖動放大電路基本設計中,因為是使用電流對負載充放電之速率來達到抖動放大,因此先針對充放電位準以及時間作定義。如表二所示。
圖十(a)中,通常抖動放大電路在低速率操作時,因其抖動量相較於半個週期時間所佔的比例較小,因此電荷幫浦輸出(1、2)到達高穩態點時間(ts1、ts2)通常會小於負緣轉態點時間tf。
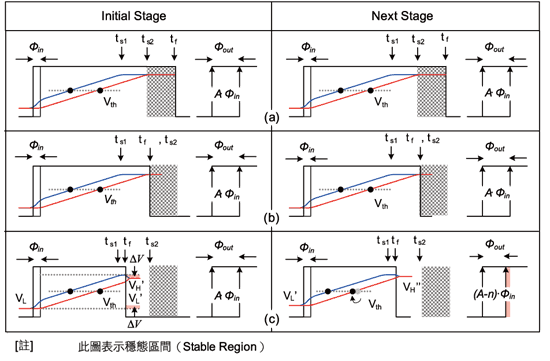
| 《圖十 抖動放大電路時序圖:(a)Case 1 : tf>ts2;(b)Case 2 : tf?ts2;(c)Case 3 : tf |
|
所以在此頻段操作因有足夠的穩態區間(stable region),其經決策電路後產生之輸出相位差OUT相較於輸入相位差IN幾乎能維持定值,也就代表放大倍率A為constant。但若當待測時脈頻率上升後,如圖十(b)所示,隨著訊號週期縮短tf之發生點提前,在tf非常接近但大於ts2時,抖動放大電路依然可勉強維持住放大倍率,所以此時即稱為操作臨界值。但假若不幸在所使用的應用中tf發生較大的變異或是操作頻率繼續往上升,導致ts2比tf晚發生,則放大倍率將開始產生非線性的變化。
從圖十(c)可觀察出在正常的操作模式下1與2最後皆會回到穩態位準VH、VL。但假若轉態邊緣tf在尚未穩定前就出現,則1與2之電壓會被強制維持在新的位準上,也就是VH’(=VH-ΔV)與VL’(= VL +ΔV)。這個現象雖對於第一個週期(initial stage)之放大倍率沒有造成影響,但是從圖中得知,在下一個週期(next stage)中因為1、2電壓起始位準點有了變化,所以經充電後與臨界電壓Vth的交點必然隨之改變。換句話說就是voltage domain variation將轉換成time domain之phase error,此時即會造成放大倍率變動。因此週期對週期抖動放大電路需操作在wide range之應用時,就必需利用一些機制控制穩態時間點ts比負緣轉態點 tf早發生,如此才不會造成放大倍率的失真。有鑑於此,本文將提出一個使用脈波吞噬觀念之單擷取量測方式來改善之。
脈波吞噬之單擷取量測方式
以上述討論可知,若要實現ts
如圖十一case1所示為一低頻操作時的示意圖。為了讓抖動放大電路的放大倍率維持定值,待測訊號的ts必需小於tf,而worst case會發生在ts等於tf的時間點,此時穩態區間幾乎會近似於零,也就是說放大倍率會非常不穩定。
為了改善這個問題,以先前的說法就必需將tf時間點做延遲。簡單來看就是把測試速度放慢,利用脈波吞噬電路移除掉0.5個週期,來換取穩態區間之寬度。如圖所示,若把case1的訊號做處理後成為TAIn1,其負緣轉態時間點發生的時間往後延遲了Δτ(=tfn-tf=Tcycle/2),這代表著穩態區間隨之放大2倍。因此若把待測訊號的頻率增加後,其因具有足夠的穩態時間,所以放大倍率將不受到clock variation和頻率變動之影響。
但在圖十一 Case2中,待測時脈訊號操作速度持續上升(約為Case1的兩倍),可以很明顯觀察到若不採用脈波吞噬機制,ts已遠遠超越了tf,此時抖動放大電路之放大倍率已為非線性操作;但若加入脈波吞噬的機制後,因待測訊號速度太快,在相同充放電的速率條件下,ts也非常靠近tfn,放大倍率變異的問題還是存在。所以由此可知真正要達到wide range的操作,不管在任何頻率下,皆需要擁有相同的穩態區間,才會真正得到constant之放大倍率。有鑑於此,我們將脈波吞噬的機制稍做修改,將不再維持固定移除0.5個週期,而是隨著待測物的頻率每增加一倍而隨之變化,其remove number可由公式二表示之:
其中N為頻率變化率。在本文中所提出的例子因為要達到數十MHz~1.6GHz之操作,所以將100MHz定為基準,頻率每增加一倍就必需改變remove number來維持放大倍率。如圖十二所示。
以電路的角度而言,要實現圖十二脈波吞噬電路其實不難,只要將待測訊號依頻段經過相對應的除頻器即可實現。但實際上若直接把待測訊號經過除頻器來達到脈波吞噬,依參考文獻[9]之說法,該訊號的抖動也同時間會被放大,約為 倍。此外,除16的電路最少需要4組DFF來實現,代表待測訊號到達抖動放大電路前就必需經過許多transistor,進而受到power noise或是thermal noise干擾導致抖動上升,這將會嚴重影響量測準確度。
以邊緣檢測達到脈波吞噬效果
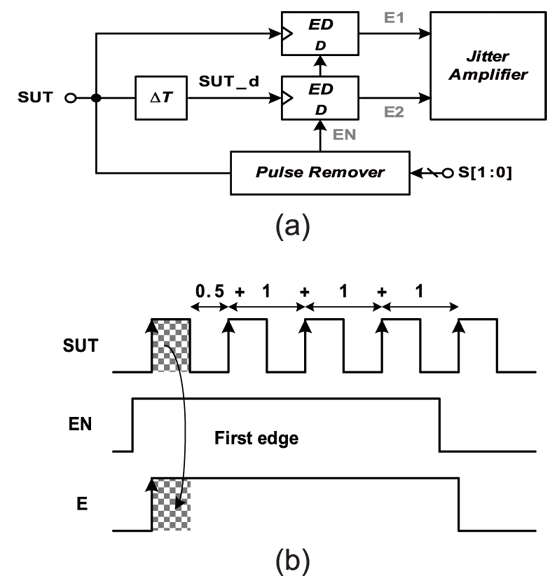
| 《圖十三 (a)所提出之抖動放大電路;(b)邊緣檢測電路操作示意圖》 |
|
因此本文將採用邊緣檢測(edge detection)之技術來達到脈波吞噬的效果,如圖十三(a)所示。其主要包含兩大方塊:邊緣檢測器與脈波吞噬電路。首先,當待測訊號啟動後,為了維持放大倍率,需先進行pulse remove的動作。以圖十三(b)為例,SUT為待測訊號,EN為脈波吞噬電路所產生,E為經過處理後的待測訊號。其中脈波吞噬電路是由MUX所實現,其可藉由控制s腳位來選擇EN訊號為SUT之/2、/4、/8、/16的結果。
此外EN接至邊緣檢測器的data input端,而SUT則接至clock input端。當EN為高電位時,SUT 正緣產生後會取樣到Hi,因此訊號E馬上pull Hi。若此時我們選擇remove為/8時,如圖十二Case3所示,EN訊號會維持4*TSUT的時間後轉為低電位,因此當SUT下一個正緣產生後,其會取樣到Low,促使訊號E pull down。
由圖中可以看出,訊號SUT經轉換後成功remove掉3.5(=4-0.5)個cycles,且SUT訊號只經過一顆ED。如此一來將可拉長stable region,維持放大倍率,並也不會因為讓待測訊號路徑太長而改變原先之抖動量。因此利用上述所提出抖動放大技術搭配脈波吞噬觀念之單擷取量測法,將可在任何頻段下線性放大待測時脈抖動,以利後段時間-數位轉換電路之抖動量解析,並解決其因製程限制所造成準確度不足的問題。
時間-數位轉換電路(Time-to-Digital Converter;TDC)
在本文中我們提出新的時間-數位轉換電路,這是因為傳統時間-數位轉換電路基本上皆是使用多級緩衝器或是延遲單元來產生多相位訊號,然後藉由取樣來得到數位碼。然而以目前0.13-um的製程來說,其所能產生的最小緩衝延遲約為25-ps左右;亦即以整個系統來看,其能測試的最高解析度也等於25-ps,此規格在現今高速應用中已無法滿足測試需求。
有鑑於此,我們將利用多工式振盪器搭配相位內插法,來實現一較高解析度之時間-數位轉換電路。如圖十四所示。其主要包含了一組多工式振盪器(Muxed oscillator)、相位內插電路(Phase Interpolator;PI)以及取樣編碼電路,當中多工式振盪器是用來產生多相位之參考訊號。相較傳統使用open loop delay chain,close loop因有回授機制,所以會具有較準確的單位延遲時間,且較不易受到製程漂移之影響。另外因為是使用振盪原理來產生相位,所以可藉由測試振盪頻推算出單位延遲時間,接著若再搭配使用內插電路技術,將可大幅提升測試解析度。
多工式振盪器是時間-數位轉換電路中最為重要的電路,因為其必需依待測訊號的上升緣,來振盪出用來被取樣之多相位高速訊號。如圖十五所示,由兩個多工器、四級延遲單元以及重置電路所組成。其稱為多工式振盪器是因為此電路具有兩種操作模式,分別為振盪模式(oscillating mode)與閂鎖模式(latching mode),模式之切換則由重置電路來決定。
相關操作原理如下。當待測訊號正緣產生時,重置電路會輸出EN為低電路,此時多工器選擇到0。以圖十五所示,此時迴路可視為一差動振盪器,持續穩定提供多相位之高速參考訊號。然而通常於各系統中抖動量皆不會超越半個週期,也就是(1/2)xUI,所以其實每個週期內的抖動測試皆會於半個週期內結束,因此只需於待測電路的半個週期裡產生出待取樣訊號。換句話說就是只需讓多工式振盪器工作半個週期後即可關閉。
因此當待測訊號負邊緣一產生,重置電路會強制EN為高電位,此時多工器將由1的路徑輸出,也就是切換至閂鎖模式。由圖中可看出,此時整體振盪迴路已被切斷,輸入即為待測訊號,各延遲單元的輸出不是待測訊號的延遲、就是待測訊號的反向延遲,直至正邊緣又產生後,才會恢復振盪模式以利抖動之測試。
傳統時間-數位轉換電路設計上,通常會受到製程所能產生的最小閘延遲所限定。為了克服此問題,我們採用了常見的相位內插電路,來產生小於一個延遲單元可提供的延遲時間。相位內插電路的直覺想法是希望能夠在兩個相鄰相位的信號之間產生一個新的信號,而其相位會介於這兩相鄰相位信號間,進而達到提供更高相位解析度的信號 [10]。
小結
以上我們介紹內建抖動測試想法與架構,主要是想藉由放大輸入抖動量來解決傳統測試法無法測試低抖動量的問題,並搭配上多工式振盪之時間-數位轉換電路,來提升整體系統解析度。此外也依電路操作特性提出一脈波吞噬電路,使得此測試系統將可於各頻段進行自我測試,將不會因操作速度而影響測試品質。接著下一章節中,我們將利用HSpice來驗證所提出之方法與架構。
(本文轉載自工研院系統晶片科技中心技術期刊第八期;作者李瑜和鄭乃楨為工研院系統晶片科技中心設計自動化技術組電路設計部副工程師,陳繼展為設計流程開發部經理)
<參考文獻:
[7]Nai-Chen Cheng et al, “A 2-ps Resolution Wide Range BIST Circuit for Jitter Measurement,” IEEE Asian Test Symposium Conf., pp. 219-223, 2007.
[8]M. Oulmane et al, “A CMOS Time Amplifier for Femto-Second Resolution Timing Measurement,” IEEE Int. Symposium on Circuit and Systems, pp. 509-512, May 2004.
[9]John A. McNeill, “Jitter in Rong Oscillators,” in Proc. IEEE J. Solid-State Circuits, vol. 32, pp. 870-879, June 1997.
[10]J. Maneatis et al, “Precise Delay Generation Using Coupled Oscillators”, IEEE J. Solid-State Circuits, vol.28, pp. 1273-1282, May 1999.>