使用頻譜分析儀量測雜訊需要很高的技巧,通常都只會以一隻指頭按下功能鍵,應用頻譜分析儀所具備的Noise量測功能「 dBm/Hz 」做量測。dBm/Hz量測功能只要用一隻手指按下就可以得到一個答案,但是如果你能不能了解Noise的特性與頻譜分析儀的原理,那你又如果判定此數據是對與否呢?利用頻譜分析儀對Noise的量測其實不難,首先你必須先了解Noise的定義,再來則是要了解頻譜分析儀的「解調器」與「RBW」的原理。如果你能了解以上的原理,對你判斷Noise的正確量測值有很大的幫助。
各種雜訊種類
雜訊的種類很多,常聽到的雜訊名詞有Random noise,White noise,Pink noise,Flicker noise等,分述如下。
White noise
即在頻譜上每Span per Hz[Span/Hz]的Noise power等於常數的雜訊。例如:20Hz到40Hz的雜訊與1020Hz到1040Hz的雜訊是相等的。一般動態電子元件的熱雜訊(Thermal Noise)大致上是頃向於White noise。
Pink noise
即在頻譜上每Power/Octave,Power/decade或頻率軸(頻寬)上等百分比(Equal-percentage)的Noise power等於常數的雜訊。例如:50Hz到100Hz的雜訊與10kHz到20kHz的雜訊是相等的。
Octave
即頻率區間2:1的區段中就叫Octave,例如:400Hz到800Hz或5kHz到10kHz區間內。
Random noise
即這個雜訊的振幅大小(Amplitude)對時間(Time)的分佈是不可預期且不會重複的,雜訊的頻譜在所有的頻率是連續的。
Sideband Noise
靠近在Carrier信號旁的雜訊。
所有的電子電路在放大器或其他的電路中,都會引進變動的雜訊。基本上計算這些雜訊的單位是以雜訊在某一電阻上變動的Vrms2來估計,Vrms2的統計值為4RkTB,因此雜訊功率的轉換是以 p=kTB瓦特(Watt)。將此單位以1 Hz頻寬(B)正規化(Normalizing),且溫度=290oK=室溫的絕對溫度(T),k=1.38(10-23波茲曼常數(Boltzmann),所以結果=-174dBm/Hz。衡量放大器或其他的電路的信號損失常用的比例單位Noise Figure(F),就是根據於理想的kBT=-174dBm/Hz為基礎的。Noise Figure(F)是一個power的比值,其公式如下:
F=(Si/Ni)/(So/No)
Si=輸入信號功率,So=輸出信號功率,Ni=輸入雜訊功率,No=輸出雜訊功率。
由定義看來是 「輸入」與「輸出」信號的信號雜訊比的比值。如果待測放大器的增益=1(Si=So)時(此種無雜訊產生的情形是不可能產生的),則F=No/Ni。此時Noise Figure(F)(NF以dB(取log)表示成下列公式:
NF=10(log(F)= 10(log(No)+ 10(log(Ni)
因為此NF是一個相對值,不容易明確的知道真正的雜訊為多少,所以我們為了得到真正的雜訊為多少,我們假設在輸入端以50(的阻抗固定之,則可以得到一個真正的功率值。所以雜訊的level變成下列公式:
Ni=kBT .........絕對溫度(T)以一般溫度室溫=290oK為基準
1Hz以外頻率單位換算法
由前面的Noise Figure(NF)定義可知,Noise Figure(NF)是以1Hz為基礎的單位。如果頻譜分析儀量測的頻率單位(RBW)不是1Hz,那要如何換算呢?
通常如果頻譜分析儀的RBW改變時,頻譜分析儀的Noise level是依下列公式進行換算:
Noise level=10(log( RBW1/RBW2)
例如,頻譜分析儀以RBW=10kHz的filter量測得到Noise=-110 dBm,則此放大器的Noise Figure(F)為何?答案如下:
NF=(量測得到的Noise level)dBm-10(log( RBW1/1)-kTBB=1
=-110-10(log( 10000/1)-174
=-24dB
一個振盪器產生的Noise分佈如何,以1996年Leeson所公佈的文獻來說,他將在載波(Carrier)旁邊的雜訊分成3個區間。在載波旁邊的雜訊,一直到主動元件的1/f點以前,依照9dB/Octave變化的區域。然後是一直到迴路的1/2 Power Bandwidth點以前的雜訊是依照6dB/Octave變化的區域。最後是結束於2FkT/1Hz的雜訊平台上。
也有其他Manassewitch的文獻主張Noise=FkT/2,所以各種主張的差距可以高達16倍(不在此多談)。頻譜分析儀對Phase比較不敏感,所以比較不適合量測Phase Noise,但是量測Sideband Noise與Random Noise是很適合的。
1.1:Random Noise的量測
1.1-1:Random Noise與RBW曲線的關係
Random Noise的量測單位是以dBm/kHz,mW/Hz來表示,也就是每頻率(頻譜)上的功率分佈。簡單的說頻譜分析儀使用的RBW filter展開的Span width所產生的Power曲線面積的平均值。圖一是一個頻譜分析儀RBW的Power曲線面積圖,我們把它畫成方格紙來計算它的面積。我們將圖一曲線下所含蓋的面積算出來約為29個方格(div2)(Voltage squared) ,而高度約為6.4格(div)。所以水平每500Hz/div 頻寬所產生的Random Noise Bandwidth(Bn)=(29 div2/6.4div)(500Hz/div=2.27kHz)。
各廠牌設計的頻譜分析儀RBW filter不盡相同,所以我們必須換算一下才能得到真正的雜訊值。圖一的RBW filter是一個6dB(B6)點為3kHz的filter,它3dB(B3)點為的頻寬為2.2kHz,因此我們可以得到此3kHz RBW f ilter與Random Noise Bandwidth(Bn)的比值。3dB點為Bn / B3=1.03 (由2.27/2.2計算得到),而6dB點為Bn / B6=0.76 (2.27/3)。舉個例子,如果你能把一台頻譜分析儀的每一個RBW曲線面積計算一下,可以得到一個Bn / B3與 Bn / B6的換算表,利用這個表可以當做你計算Random Noise的依據。表一是Tektronix 7L5頻譜分析儀的RBW比例表。@表格:表一 Tektronix 7L5 RBW與NoiseBW的比值
RBW 規格 |
30kHz |
10kHz |
3kHz |
1kHz |
300Hz |
100Hz |
Bn / B3 |
0.95 |
1.02 |
1.03 |
1.1 |
1.05 |
1.0 |
Bn / B60 |
.78 |
0.85 |
0.76 |
0.73 |
0.74 |
0.70 |
Random Noise
一般來說頻譜分析儀的filter在量測Noise都將3dB filter的修正因子定訂為1,而將6dB filter的修正因子定訂為0.76,這是依照Gaussian(高斯)filter來定訂的。然而現在的頻譜分析儀所設計的RBW filter,可能只是4 Synchronously tuned filter或是6 Synchronously tuned filter的設計,而不是無窮大的Gaussian(高斯)filter。但是由表1.1.1-2大致上可以看出4 Synchronously tuned filter 以上的值與Gaussian(高斯)filter曲線的誤差不大。Tektronix 7L5 的RBW filter也大致相同。
表二 理論上各filter的Random Noise Bandom
Synchronously tuned number of sections |
B6 / B3 |
Bn / B3 |
Bn / B6 |
1 |
1.732 |
1/571 |
0.907 |
2 |
1.554 |
1.220 |
0.785 |
4 |
1.480 |
1.128 |
0.762 |
6 |
1.457 |
1.105 |
0.758 |
10 |
1.439 |
1.087 |
0.755 |
Gaussian(infinite) |
1.414 |
1.064 |
0.753 |
2 Maximally flat 2-uples per CISPR EMI spec. |
1.247 |
1.037 |
0.832 |
Random Noise的量測在Rayleigh分佈的修正
不管頻譜分析儀的處理過程來說,最後一定要經過包封檢波器(envelop detector)才能將信號檢出。雖然雜訊在這些頻譜分析儀的混波(Mixer),放大,衰減過程中可能都是Random Noise的分佈顯現。而Random Noise 是依照常用的平均分佈(Normal distribution),不會有所偏差(依(值均勻分佈) (圖二) ,圖三 A部份是Rayleigh分佈曲線,由於它利用數位示波器的以Zoom功能放大取樣出頻譜分析儀的雜訊,可以看出中心平均值一邊偏移的分佈,與上面的Rayleigh分佈曲線相符合)(圖三)。圖四上半部是頻譜分析儀linear mode(V)的雜訊分佈,可以看出雜訊信號在螢幕上方較為稀鬆為Rayleigh分佈曲線,圖下半部是示波器的雜訊為平均分佈圖,趨向於均勻分佈。(圖四)
頻譜分析儀的雜訊分佈是經過包封檢波器後,而變成Rayleigh分佈的。而圖三則是Rayleigh分佈的曲線分佈P(R)=(R/(2)e(-R( R /2((()。Rayleigh分佈的平均值與標準差(已經偏移與平均分佈(不同了 。Rayleigh分佈的(值與平均分佈的Average值的RMS偏離度(deviation)關係可以下列的公式來表示:
RMS =(((/2
而Rayleigh分佈的RMS=(((/2,所以兩者的比值為
(4/(=1.13 ( 20(log(1.13)=1.05dB
所以Rayleigh分佈的RMS值會比頻譜分析儀用Average功能的量測值高1.05dB。量測Random Noise一般會經過頻譜分析儀平均(Average)的功能,所以頻譜分析儀將信號濾出的過程是先經過log電路,再取平均。這個過程與先經過平均,再取log是不同的。log電路的作用是將大信號變小,小信號變大,所以在輸入信號較大時IF放大器降低放大增益,而在輸入信號較小時IF放大器增加放大增益。所以除了取平均的修正值為1.05dB外,還需修正log mode的誤差1.45dB。
我們常常看到量測Random Noise的結論是:使用頻譜分析儀的linear mode量測Random Noise時要修正1.05dB。而使用頻譜分析儀的log mode量測Random Noise時要修正2.5dB,是由1.05dB+1.45dB得到的。
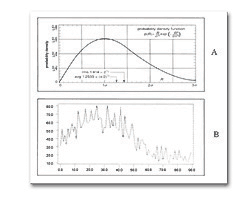
| 《圖三 中心平均值與上面的Rayleigh分佈曲線》 |
|
RBW設定對Random Noise量測的影響
我們知道當頻譜分析儀的RBW改變時,頻譜分析儀的Noise level會跟者RBW filter依10(logB1/B2而改變。所以Dynamic range可以因RBW變小而得到改善。那麼量測Random Noise是不是也會受到影響呢?答案是Random Noise不會受到RBW改變的影響,它的值一定會相同的。
圖五的上面曲線是不加Video filter所得到的圖形,由圖中可以知道頻譜分析儀量測到的是Peak值,它是依照Rayleigh分佈出現的peak值,如果你用Max Hold(記下最大值)的功能將最大值記錄下來,可能會得到更大的數值。圖五的下面曲線則是加入Video filter=300Hz得到的圖形,兩者相差約10.4dB。我們啟動頻譜分析儀的Random Noise量測功能(dBm/Hz)與Average功能,量測出Random Noise=-101.3dBm/Hz(圖六的左上角圈圈內數值)。
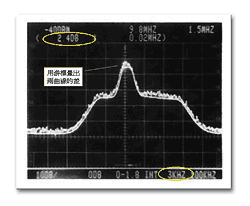
但是現在如果改變設定Video filter=3kHz,你會得到的圖七上面的曲線。(圖七)可以看出與原來300Hz的曲線(下面的曲線)相差約只有2.4dB,與前面圖七的結果10.4dB不同。可以知道如果使用的Video filter不夠小的話,可能所使信號濾過得不夠完全會得不到真正的Random Noise曲線(Video filter=300Hz的圖形)。那麼Video filter與RBW filter的設定如何才能得到真正的Random Noise數值呢?
如果我們更改RBW=1MHz改變頻譜分析儀的Noise level且再次啟動Random Noise與Average量測功能,我們從圖九的結果可以看出上面的圖形已經變形(圖形頸部的頻寬已經由2.13MHz變成2.89MHz)與原來的答案一定不一樣。
綜合以上的結果我們可知,如果filter不夠小以致於無法將信號處理平滑(Smoothing),你得到的結果會如圖五上方的曲線或圖七上方的曲線圖形。那麼filter的值要設定為多少才能得到真正的曲線呢?規則就是:RBW filter的BW設定必須大於量測頻寬的1/3。此例子中頸部的頻寬=2.13MHz,則RBW filter的BW設定不能小於700kHz。
filter對量測產生的誤差
以圖五上面曲線是依Rayleigh分佈出現的peak值,這個peak值與真正Random Noise 平均值的誤差是多少呢?
由前面10.4 dB的誤差,經由10(logR=10.4公式可知R(Ratio)=3.3。由於Rayleigh分佈與平均分佈的標準差(相差為1.25,所以Peak值=3.3(1.25=4.13。代入Rayleigh分佈的公式P(R)=(R/(2)e(-R( R /2(((),因為分佈的曲線都會等化成面積趨近於1,所以會Rayleigh分佈的公式會趨近於1-e(-R( R /2((()。
而-e(-R( R /2((()就是產生的誤差,-e(-R( R /2((()=-e(-4.13( 4.13 /2)=0.02%。根據Sutcliffe於1972年發表的論文「Relative Merits of Quadratic and linear Detectors in the dircet Measurement of Noise Spectra"中提出,Video filter不足的Smoothing與Average所得到的誤差為(2BV/Bn)1/2。如果我們假設使用的Video filter 是Noise頻寬的1/100,則誤差為(2/100)1/2=0.14。14%的誤差不可謂不大。所以我們使用Video filter的另一個指標就是:Video filter的頻寬必須為量測Noise Bandwidth的1/300。
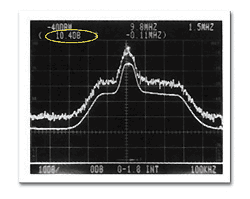
| 《圖五 不加Video filter所得到的圖形》 |
|
Random Noise與「頻譜儀內部雜訊差很大」的量測
我們得到正確的Noise圖形後,是要算出在曲線下面的Power有多少,如果曲線變化不大的話算出面積是沒有甚麼問題,但是如果曲線變化很大的話就是傷腦筋的問題了。以圖1.1.3-2的圖形來說,我們可以將圖形等化成圖1.1.5-1。我們對方形的面積的計算是沒有問題的,但是圖中有許多的三角形或梯形又要如何呢?梯形我們可以將它分割成2個三角形+1個方形,這也是沒有問題的。但是三角形就是我們要處理的問題了。我們看圖九中的放大圖形,假設三角形Y軸的長度=-b(dB),X軸的長度=a(Hz),則P(dB)=(-b/a)f,而P(dB)=10(logP,所以P(f)=10-(b/10a)f。
我們也知道10X=eX/0.4343,所以P(f)=e-(b/4.343a)f,e是自然對數。在曲線下的面積可由積分得到P(total)=0(a e-(b/4.343a)f dt=(4.343a/b)[1- e-b/4.343]。
三角形面積Y軸(dBm)的積分是趨近於 無窮大 ,而eX=1+X+X2/2!+X3/3!,當b趨近於0時P(total)=a。
圖九最上層梯形的三角形b=19.2dB(高),a=0.75MHz[(2.1-0.6)2=0.75],可算出三角形的面積=(4.343(0.75)/19.2[1-e19.2/4.343]=0.1676MHz。梯形兩邊個各有2個三角形,所以梯形的面積=(0.1676(2)+0.6MHz(方形)=0.935MHz。此梯形產生的Noise Power為-101.3dBm/Hz+10(log0.935MHz=-41.6dBm。
同理計算下一個梯形為上底 =2.1MHz,高為3.6dB(22.8-19.2)的梯形的面積,它可以分成2.9MHz與1.5Mz的2個三角形加上一個2.1MHz的方形。所得到的面積為1.97MHz與1.02MHz,此梯形產生的Power為-101.3dBm/Hz-19.2+10(log(1.97+1.02)MHz=-55.7dBm。
同理最下面的梯形產生的Power為-64.5dBm。
如果我們把-41.6 dBm當做=1,那麼-55.7dBm與-64.5dBm的比例分別為0.039與0.005,所以總共為1.044。此0.044對-41.6dBm的貢獻為0.2dB,此0.2dB對整體的影響不會很大,所以無須做修正。
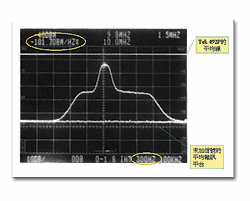
| 《圖六 頻譜分析儀啟動Random Noise與Average量測功能的結果》 |
|
Random Noise與「頻譜儀內部雜訊差很小」的量測修正
如果量測的Noise太低,會與頻譜分析儀內部的雜訊混在一起,產生很大的誤差。例如:Noise=頻譜分析儀內部的雜訊會有3dB(10(log(1+1)=3dB,量測雜訊與頻譜分析儀內部的雜訊各貢獻一半)的誤差。所以量測的Noise太低應予以修正量測值,才能得到正確的NoisePower值。一般來說量測雜訊信號如果與頻譜分析儀內部的雜訊相差在10 dB以內,則必須加以修正。以圖十為例將量測的游標下降到與頻譜分析儀內部的雜訊差8dB的位置,必須將讀值修正,修正的值可以參考表三。由查表可知需修正0.75dB,實際的Noise值=7.25dB。
表三 量測修正值
量測值比內部的雜訊最大值 (dB) |
1.5 dB |
2 dB |
2.5dB |
3dB |
4dB |
5dB |
6dB |
7dB |
8dB |
9dB |
10dB |
Noise 的真值比內部雜訊最大值 (dB) |
-3.9 |
-2.3 |
-1.1 |
0 |
1.8 |
3.35 |
4.74 |
6.03 |
7.25 |
8.42 |
9.54 |
真值比內部雜訊最小值 (dB) |
5.35 |
4.33 |
3.01 |
3.01 |
2.2 |
1.65 |
1.26 |
0.97 |
0.75 |
0.58 |
0.46 |
由於表三的數值是依頻譜分析儀內部的雜訊為比值所得到的,可類推至其他量測值比內部的雜訊上。
例如:
1.量測值比內部的雜訊大3dB;
10(logX=3,所以X=2,10(log(2/2-1)=3.01。
2.量測值比內部的雜訊大2dB;
10(logX=2,所以X=1.585,10(log(1.585/1.585-1)=4.328。
| 《圖七 設定Video filter=3kHz的量測結果》 |
|
相對準位Random Noise雜訊的量測
數位傳輸信號在頻譜分析儀上看起來好比Noise一樣,FCC(Fedral Communcation s Comission)協會對此種頻寬的上限有所限制,是以頻寬佔據率(Spectrum bandwidth Occupancy)來規範。FCC協會對數位傳輸信號頻寬違規有一個規範,低於15GHz的Digital radio transmission Spectrum 所佔用的頻寬量測位置如圖十一。我們將其結果以FCC協會11GHz數位傳輸信號的Mask規範畫出會如圖十二的Mask。
而FCC協會6GHz的數位傳輸信號則與11GHz的Mask有一點不同,在頸部的頻寬=30MHz。不管如何頸部位置的頻寬是以4kHz的RBW來規範 (圖十二是11GHz數位傳輸信號頸部40MHz,-51dB)。
雜訊的單位為dBm/Hz,雜訊的dBm會隨RBW而改變,但是經過頻寬/Hz規格化後dBm/Hz是不會變的。例如前例中的讀值-101.3 dBm/Hz,如果以1kHz的filter來量測得到的數值會=-71.3 dBm/Hz(-101.3+10(log 1000=-71.3),以4kHz的filter來量測得到的數值會=-65.3 dBm/Hz(-101.3+10(log 4000=-65.3)。
dBm/Hz是不會變的已不是問題了,重要的是你要知道在那裡量測「Mean output power」。甚麼是「Mean output power」?以FCC的Mask來說,相對於Mean output power的關係如圖十一。FCC規定的公式為
A=35+0.8(P-50)+10(logB
A=從Mean Output Power level點算下來的衰減量(dB)。
P=從Carrier點算下來衰減80 dB時對Carrier的調變%。
B=FCC規範的頻寬。
例:以一個6GHz的發射機來說,信號要衰減到80 dB以下的話,此時的調變率%=87.5%(或者30 MHz (0.875=26.25MHz)。
A=35+0.8(87.5-50) +10(log30=79.77 dB
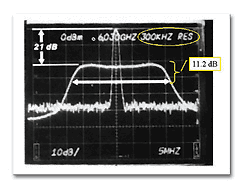
一個比較簡單的方法是,如果我們可以知道Carrier的power level,則我們可以將它當做參考的Mean Output Power的起使點。但是如果不知道的話,也可以由廠商所給的資料得知。例如:圖十三是以一個11GHz載波上面載上 30.086MHz的信號速率(Signaling rate)來說,我們可以由公式10(log(fs/4kHz) 計算出相對的位置。10(log(30.086MHz/4kHz)=38.8dB,38.8dB與規範的51dB位置相差12.2dB,所以信號頻寬要由信號頂端往下12.2 dB的位置計算,由圖十三可知此處的頻寬為39MHz。
圖十四是另一個例子;我們知道6GHz 載波(Carrier)的Power level,則我們將它當做Mean Output Power的參考位準。經過數位調變後信號往旁邊分散下跌21dB,而此時頻譜分析儀所使用的RBW=300kHz。我們要將此值換算成規範中的RBW=4kHz時的dB值:21+10(log(240/4)=38.8 dB
此處的240是由300kHz((6dB RBW filter的雜訊修正因子=0.8得到的))。所以我們量測點應在相距數位調變信號頂點11.2dB(50-38.8)點的頻寬即為依規範的50 dB點的頻寬"30MHz(箭頭內之頻寬)。