Delta-Sigma(Σ-Δ)ADC在連續訊號採集,高精度測量等領域被廣泛應用。本文從量化雜訊、訊噪比、過取樣等概念出發,分析Delta-Sigma ADC的工作原理,並詳述如何透過取樣、數位濾波消除量化雜訊,進而實現高解析度;並且介紹如何在Digi-Key網站中透過參數篩選快速進行Delta-Sigma(Σ-Δ)ADC選型,並提供實際的應用案例。
你可能會知道Delta-Sigma(Σ-Δ)ADC可以達到很高的精度,但它具體是怎麼實現的?本文將從量化雜訊、訊噪比、過取樣等概念出發,分析Delta-Sigma ADC的工作原理。
讀懂ADC的基本概念
我們在瞭解Delta-Sigma(Σ-Δ)ADC原理之前,先明確幾個概念:
1.量化雜訊
下圖中,藍色斜線是連續的類比訊號,階梯狀波形是經過ADC轉換後的離散訊號。如果我們把這個兩個相減,會得到右邊那個像鋸齒波一樣的量化誤差。
量化雜訊(Quantization Noise),這裡Q值代表量化,如果取樣越快,兩個Q之間的距離越小,Q的幅值越低,也就是量化雜訊的幅值越低。雖然Q值幅值變低,但是它包圍的面積不變。因此,改變取樣速度,可以改變量化雜訊的幅值,但不能改變量化雜訊的總能量。
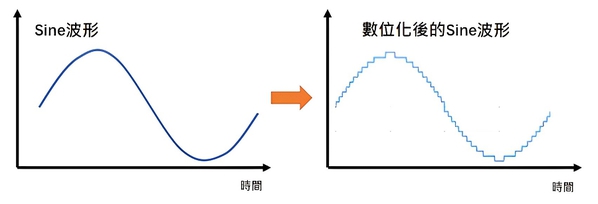
| 圖二 : 數位化後的Sine波形(source:TI) |
|
從時域裡看,對於一個類比的Sine波形,經過ADC轉換數位化後,我們會得到鋸齒狀的Sine波形。我們加快取樣速度,可以把鋸齒變得很細,但是依舊存在,並且量化雜訊的總能量不變。
2.訊噪比
如果把上面的Sine波形放到頻域裡看。我們希望訊號頻率的幅值儘量大,而雜訊幅值儘量小。
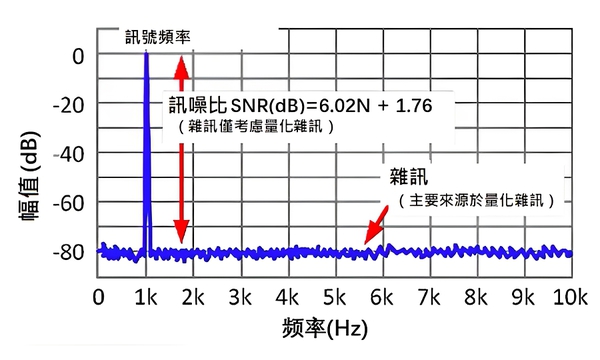
| 圖三 : Sine波幅頻相應曲線(source:TI) |
|
圖三的雜訊主要來源於量化雜訊,透過訊噪比計算,會得到一個固定的公式:
訊噪比SNR(dB)=6.02N + 1.76(雜訊僅考慮量化雜訊)
‧ SNR:指的是量化雜訊訊噪比(Signal noise ratio)
‧ N:指的是ADC取樣位數。如果把N提高,訊噪比提高,即訊號更大,雜訊更小。取樣品質變好,因此,提高ADC取樣位數,可以提高取樣品質。
一般來說,提高取樣位數,往往意味著ADC的成本可能也會更高。
有沒有不提高位數,同樣最佳化訊噪比的方法呢?答案是「有的」,那就是過取樣。
3.過取樣提高訊噪比
我們把圖三進一步簡化。下圖的紅色箭頭表示主訊號的幅值,灰色代表雜訊幅值,平均分佈在DC到fs/2之間。(fs為取樣頻率)
如圖四,如果將取樣速率提高K倍,雜訊能量不變,並且平均分佈在更寬範圍,進而雜訊的幅值降低。原始訊號沒變,但是雜訊幅值減少,也就是訊噪比提高了。提高取樣速率之後的訊噪比公式:
SNR=6.02N+1.76dB+10log(OSR)
其中,過取樣速率OSR =Fs/(2xBW), BW為頻寬。(注意:此公式僅適用於只存在量化雜訊的理想ADC)
因此,提高取樣速率有助於提高訊噪比。
我們可以在Digi-Key網站中類比數位轉換器(ADC)大類下,在架構選項找到「三角積分」,即Delta-Sigma ADC。
可以透過參數來篩選ADC。比如透過ADC取樣位數、取樣速率等關鍵參數來篩選合適的ADC:

| 圖六 : 在Digi-Key網站中透過參數篩選查找ADC |
|
Delta Sigma調製的原理
Delta Sigma調製,即把類比訊號調製成方波形式的PCM(Pulse Code Modulation)訊號。PCM波是一個頻率固定占空比變化的波,透過比較訊號和高頻調製波產生。然後經過數位濾波,再透過解調,得到一個數位化的最終結果。
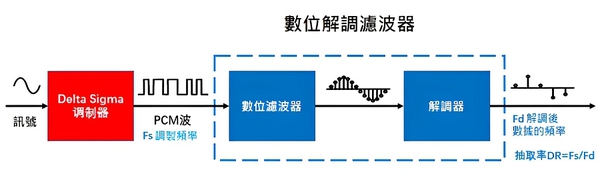
| 圖七 : Delta-Sigma(Σ-Δ)ADC原理 |
|
其中數位解調濾波器可以和調製器一起整合在Delta Sigma ADC裡面。也可以把Delta Sigma調製器部分做成一個獨立的調製晶片,然後把數位解調濾波器整合在MCU裡,比如TI C2000。
解調的過程其實是根據一定比率對訊號進行抽取,抽取率DR=Fs/Fd。
‧ Fs為調製頻率
‧ Fd為解調後的頻率
以下重點說明Delta Sigma調製器的工作原理與數位濾波器:
Delta Sigma調製器的工作原理
透過Delta Sigma調製器調製,我們把類比訊號調製成方波形式的PCM訊號。
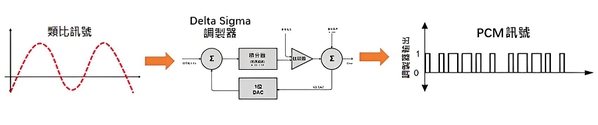
| 圖八 : Delta-Sigma調製器輸出(時域) |
|
我們想像一下啊,下圖類比訊號(紅色虛線)和PCM訊號(黑色方波狀的波形),表達的是同一個訊號。
Delta Sigma調製器傳遞函數
透過上面的迴路,進行Delta-Sigma數位化調製。
迴路的傳遞函數,輸出等於輸入與輸出之間的差值乘以前向的積分環節加上量化雜訊。我們可以得到傳遞函數:
Dout=(Vin-Dout)A(f)+e(n)
求解這個傳遞函數,得到輸出Dout
我們可以看出,(f/(1+f))對於量化雜訊e(n)相當於一個高通濾波器,而(1/(1+f))對於輸入訊號Vin相當於一個低通濾波器。
經過Delta-Sigma調製環節之後,訊號被最佳化,在頻域範圍內更好理解。
當頻率較低時,訊號保留,量化雜訊被削減,當頻率比較高時,量化雜訊保留,訊號削減。
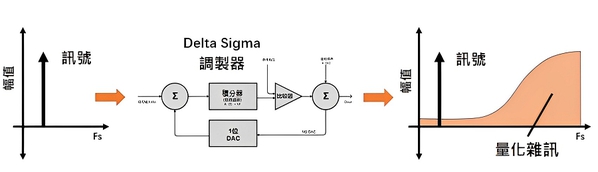
| 圖十二 : Delta-Sigma調製器輸出(頻域) |
|
因此,透過Delta-Sigma調製環節之後,有效訊號頻帶的訊噪比進一步被最佳化。
數位濾波器
透過Delta-Sigma調製器之後,我們還需要進一步數位濾波。
下圖是經過Delta Sigma調製器之後的幅頻特性,如果設計一個如圖中紅線所示的數位濾波器(比如一個低通濾波器),把紅線右邊的高頻雜訊濾除,那麼剩下就是有效的訊號資訊。
而數位濾波器的頻寬,幅頻特性,我們可以用參數或者階數去調節。
常用的兩種濾波器,可以實現要的幅頻特性:
以下使用實例說明:TI ADS1672晶片使用55階的FIR(Finite Impulse Response,即有限脈衝響應),實現了寬頻通帶濾波器的功能,同時意味著,需要延遲55個時鐘週期來完成濾波。
一般來說,階數越高,幅頻特性越好,量化雜訊衰減越厲害。但是,階數越高,帶來的延遲也越大。所以,在更好的幅頻特性還是要更快的響應,有時不得不取捨。
以ADS1672EVM-PDK為例,24位元,78.1k ~ 625k取樣速率,包括ADC評估軟體ADCPro,內置分析工具,包括示波器、FFT和長條圖顯示等,能夠節省設計階段。
結語
Delta-Sigma(Σ-Δ)ADC可以達到很高的精度,需要過取樣、數位濾波消除量化雜訊,進而實現高解析度。而這樣做的代價是犧牲了取樣速度,延遲變大,功率消耗也不小。基於這樣的特性,Delta-Sigma(Σ-Δ)ADC在連續訊號採集,高精度測量等領域有著廣泛的應用。
(本文作者Barley Li為Digi-Key Electronics亞太區技術內容部門應用工程經理)