病患、周日烤肉、淋浴或水族箱用水—在這些情況下,越來越多的人採用數位溫度計而不是類比溫度計來測量溫度。溫度感測器的選擇對開發工作具有決定性的作用。一款免費的模擬程式使得這項任務變得更加容易,同時也有助於節省時間和費用。
在開發數位溫度測量電路時,必須首先確定在純機械方面的設計。不過,本文不會討論這些事項。接下來就是考慮電熱(electro-thermal)方面的事項,在這方面,需要先回答以下的問題:
‧ 預期的溫度範圍是多少?
‧ 需要哪種級別的測量精度?
‧ 使用哪種類型的溫度感測器?
‧ 感測器的電氣特性容差有多大?
‧ A/D轉換器應提供的最小位元率是多少?
‧ 感測器的訊號取樣率要多高?
‧ 在應用中所有其他被動組件的數值和容差有多大?
確定溫度範圍和測量精度十分重要,因為它們決定了後續的步驟。例如,這個案例中的溫度範圍應為攝氏+ 25度至+ 150度,整體精度必須為+/-2度。在這種情況下,可以使用的溫度感測器有兩種:一種是高靈敏度但非線性的熱敏電阻,另一種則是電阻溫度裝置(RTD),比如鉑溫度感測器,它是線性的,但靈敏度較低。
選擇合適的感測器:不是容易的決定
選擇合適的感測器時,確定哪一種感測器可用來達到所需的規格是很重要的。單單回答上面所列出的每道問題是不夠的。各參數之間會表現出複雜的相互作用,即使它們互相影響。
通常來說,一個系統的限制因素決定了測量的準確性。如果這是未知的,將剩餘參數的容差降低到接近零幾乎是沒有作用的。例如,如果是以進行精度優於攝氏+/-0.2度的溫度測量為目標,而採用精密的熱敏電阻,同時也用了一款簡單的8位元A/D轉換器,就會顯著降低熱敏電阻的測量精度。反過來也是如此:如果使用中等精度的感測器,24位元A/D轉換器的應用便沒有很大的意義了。如果要檢測最小的溫差,建議使用具有高微分線性的ADC和校準演算法。
另一種實現最精準測量的方法是使用具有線性溫度特性的A級鉑感測器(在攝氏零度時為攝氏+/-0.15度)。然而,其溫度係數低於熱敏電阻的溫度係數,即必須放大測量訊號。但這需要額外的硬體並帶來更多的容差。
顯然,這使得組件的選擇成為一項複雜的任務,通常需要進行大量的測試才可完成。這很耗時間和金錢。如果可以選擇具有一定容差的感測器、A/D轉換器精度和其他硬體組件,設置「虛擬原型測試系統」,並且進行的模擬操作可以即時顯示可實現的精度,那麼這項工作就會更容易、更快捷。
基於PSpice的模擬程式正好可以滿足要求,它們大多是免費的,即便它們是類比的模擬軟體。由於PSpice及其眾所周知的「輕型」版本可以模擬數位溫度計的任何流程,如圖一所示(儘管看起來與基於RTD的電路相似,但這其實是基於熱敏電阻的電路)。
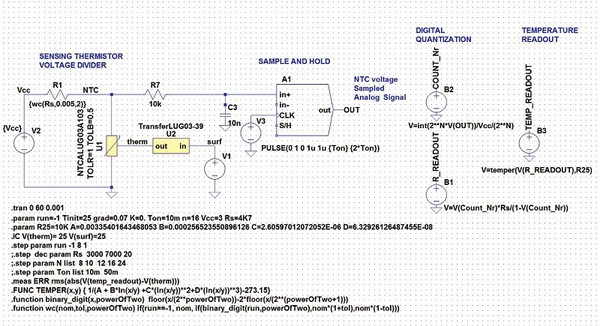
| 圖一 : 數位溫度計的簡化模擬電路圖(source:威世) |
|
數位溫度計的組件
不管你是選擇NTC(負溫度係數)熱敏電阻還是鉑RTD作為溫度感測器,這些組件的SPICE模型都很容易找到。此外,該電路包含一個由熱敏電阻和一個固定電阻組成的分壓器,低壓電源提供測量電流。在放大並通過適當的ADC進行濾波後,由此產生的電壓將被數位化。理想的組件是JRC的新款類比前端(NJRC9103),它可以直接連接溫度感測器。這款類比前端(AFE) 可直接提供數位資料,還提供各種用於偏移補償的校準功能,微處理器可利用它來計算溫度。
直接暫態電路模擬(圖二)顯示了應用的溫度曲線、感測器的延遲和斜率回應以及訊號的數位化。可以在圖中下半部分看到讀出溫度的時間偏差。為了更容易識別數位化,我們選擇了10位元的低A/D轉換器解析度為和長達200ms的採樣時間,用於模擬操作。
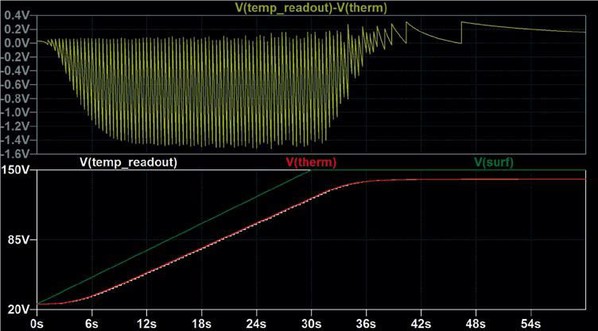
| 圖二 : 直接暫態電路模擬顯示了應用的溫度曲線。上半部分:外部溫度Vsurf,熱敏電阻溫度Vtherm和數位化測量值(ton = 200 ms, n = 10)。底部窗口:測量值與實際熱敏電阻溫度之間的差異。(source:威世) |
|
可以使Spice輕鬆地進行模擬感測器的特性和容差,如本範例中使用的威世NTCALUG系列10kΩ NTC熱敏電阻,以及固定電阻。借助類比行為建模電壓源,執行訊號的數位化和數位化原始測量資料轉換到溫度的運作。有趣的是,A/D轉換器的位元數(n)現在是模擬操作的一個參數,並且可以在8和24之間變化。採樣/保持模組(sample/hold module)的採樣時間(tone)也是可變參數。使用Sigma Delta ADC時,可以省去外部的採樣/保持,特別是因為溫度變化通常發生在100 ms範圍內。
在此範例中,10ms採樣時間是第一個需要設置的參數。然後可以通過輸入8到24位元之間的值來確定理想的A/D轉換器解析度。當計算誤差函數作為讀出溫度和熱敏電阻溫度之差的有效值時,在n>16解析度下誤差不會進一步降低,如圖三所示。
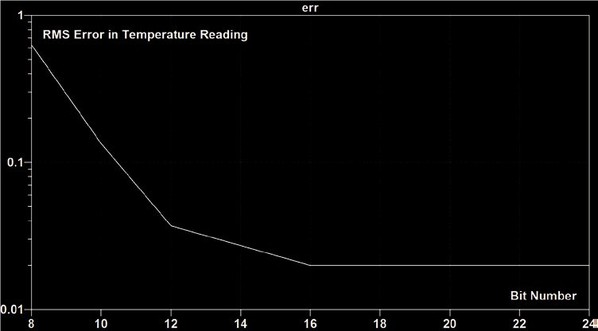
| 圖三 : A/D轉換器解析度高於16位元時,讀出溫度與熱敏電阻溫度之間的差值保持不變。(source:威世) |
|
或者,也可以最佳化串聯電阻器R1以實現最小誤差值。圖4說明了Rs串聯電阻的誤差函數在4.7 kΩ時達到最小值。在SPICE的指令中定義了ERR(錯誤)函數 (圖四),用於模擬操作。
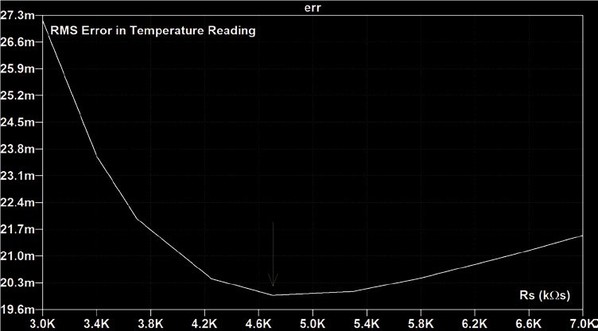
| 圖四 : 在串聯電阻為4.7kΩ時,誤差函數達到最小值。(source:威世) |
|
在下一步驟中,改變熱敏電阻和固定電阻器R1的容差,並且針對每個容差執行基於這些容差的最壞情況分析。
圖五至圖七顯示了三種情況:圖5顯示了NTC的結果,其中dR25/R25 = +/-1%,B25/85容差為+/-0.5%,結合威世的0.5%薄膜TNPW系列扁平晶片電阻器。在這種情況下,測量不確定性從攝氏25度時的+/-0.4度增加到在攝氏100度時的+/-1.5度。這種模擬適用於最壞情況。考慮到NTC的R25和B25/85容差以及固定電阻R1的容差,可以得到23 = 8範例的容差,白色曲線是參考曲線。圖5中的模擬數值顯示容差值是均勻分佈的,這意味著,電阻器彼此的相對容差的選擇是適當的。
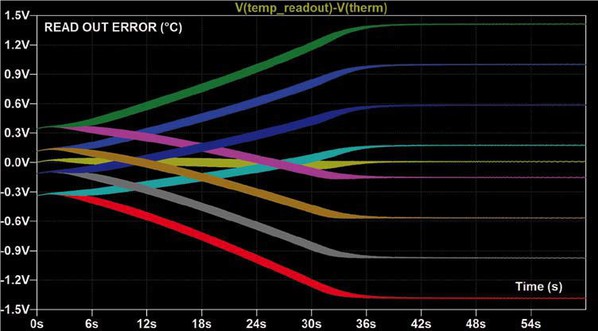
| 圖五 : 溫度測量不確定性,NTC的dR25 =+/-1%,dB =+/-0.5%,固定電阻的為+/-0.5%。(source:威世) |
|
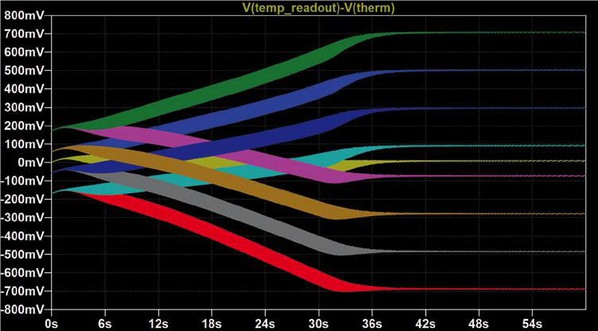
| 圖六 : 如果所有電阻容差減半,溫度測量不確定性也會減半。(source:威世) |
|
圖6顯示,將所有電阻容差減半,溫度測量不確定性亦可以減半(熱敏電阻為R25 = 0.5% 和 B25/85 = 0.25%,固定電阻則為0.25%)。然而,這有點過於激進了,因為我們懷疑是否所有電阻供應商都能夠保證B25/85值為+/-0.25%。比如,B25/85係數的常見值是+/-1.5%。如果使用與圖5中相同的數值執行相同的模擬操作,而B容差為±1.5%,可以達到圖7中所示的結果。由於高溫下的測量誤差相對較大,它們說明了這是一個不盡理想的設計。我們還可以清楚地看出,最壞情況分析的容差值結果分佈也不理想。
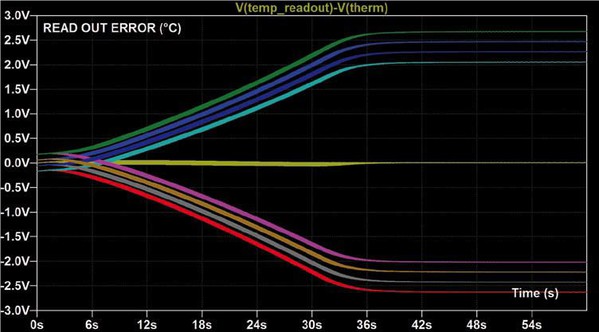
| 圖七 : NTC的溫度測量不確定性dR25 = 0.5%(但dB =+/-1.5%),固定電阻容差為+/-0.25%。(source:威世) |
|
這說明:可以使用相對簡單的模擬電路,並按照組件參數將溫度測量電路的整體精度視覺化,這是進行額外實驗以減少開發時間和成本的理想起點。
(本文作者Bert Weiss為儒卓力電阻器產品技術支援、Alain Stas為威世非線性電阻產品行銷工程師)