大部分新型的頻譜分析儀都提供一項方便的量測,可決定正弦信號在各種偏移頻率下的整合相位偏差(integrated phase deviation)。量測結果可以dBc或度為單位表示。本文將說明如何根據單旁波帶相位雜訊功率與載波比(dBc),來計算RMS相位偏差(以度為單位)。這項資訊有助於瞭解量測結果及進行量測最佳化。
首先,我們會討論角度調變信號(angle modulated signal)的調變指數與Bessel函數曲線間的關係。
經過正弦調變的相位調變載波之頻譜
角度調變信號,例如相位和頻率調變,可以調變指數m來描述。頻率調變信號的調變指數為峰值頻率偏差與調變頻率的比值。相位調變信號的調變指數,則為峰值相位偏差Δφpeak。公式一說明了這項關係。
以頻率為fmod的正弦信號對頻率為Fc的載波進行角度調變,將會在載波頻率Fc附近,產生以頻率fmod間隔的無限個旁波帶。調變載波與旁波帶的振幅,可利用信號的調變指數和Bessel函數J0-Jn的曲線來決定。
圖一顯示Bessel函數J0至J3的曲線。在調變指數為3的位置劃一條垂直線,相當於3度的Δφpeak。該垂直線與Bessel函數的各條曲線的交叉點,在電壓刻度上指出了調變載波和旁波帶與未調變載波的相對振幅。
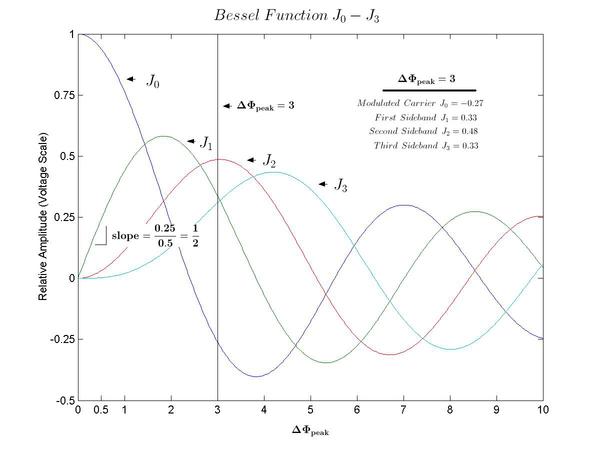
| 圖一 : Bessel函數曲線可用來決定角度調變信號的頻譜。 |
|
在圖一的範例中,我們得到下列的相對振幅:
- 調變載波 J0 = –0.27
- 第一個旁波帶 J1 = 0.33
- 第二個旁波帶 J2 = 0.48
- 第三個旁波帶 J3 = 0.33
圖二是調變頻率fm為400 Hz,峰值相位偏差為3度時,相位調變信號載波Fc在1 GHz頻率下的頻譜。振幅刻度單位為伏特(V),未調變載波的振幅設為100 mV。黃色軌跡為未調變載波的頻譜,藍色軌跡為調變信號。調變載波和前三個旁波帶的標記讀值,很接近J0 到J3的預測值。請注意,此為頻譜的幅度,所以Bessel函數的負值會顯示為正值。
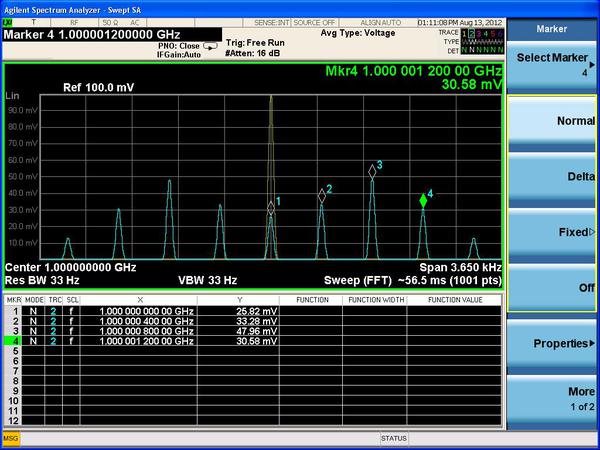
| 圖二 : 使用安捷倫X系列信號分析儀,所得到的角度調變信號的頻譜。 |
|
以經過正弦相位調變的載波之頻譜來決定rms相位偏差
在頻譜分析中,還必須根據信號頻譜來決定Δφpeak。大的Δφpeak值會有點難決定,但檢視Bessel函數的曲線可以發現,對小Δφpeak值(Δφpeak < 0.5度)來說,調變載波和未調變載波的振幅幾乎相等,且第二級和更高級旁波帶的振幅接近於0。
還有一項優點可以大幅簡化這項作業,那就是以小峰值相位偏差而言,第一個旁波帶的相對振幅幾乎等於峰值相位偏差的1/2。相位雜訊的Δφpeak很小(< 0.5度),故可使用這三個係數,按照公式二中的簡單關係,來量測第一個旁波帶的相對振幅與調變載波的振幅之比值,以決定Δφpeak。
大部分新型頻譜分析儀的振幅值,都以功率刻度顯示而非電壓刻度。因此,可使用公式二將其轉換成公式三中的相對功率。此外,大部分頻譜分析儀提供的相位雜訊結果都是rms相位偏差(Δφrms),而非峰值相位偏差(Δφpeak)。所以公式四將峰值偏差轉換成rms。最後,公式五顯示載波經正弦信號調變後,以相對功率刻度量測所得到的rms相位偏差。
根據載波的相位雜訊來計算整合相位偏差
這項計算必須經過量身訂製,才可根據相位雜訊來量測整合相位偏差。為達此目的必須加入L(f) 項,它是信號的單旁波帶相位雜訊中相對於載波振幅的功率之雜訊密度。用來決定相位雜訊的方法為整合頻寬法(integrated bandwidth method)。
使用者必須選擇一個偏移範圍 -- 間隔的fstart到fstop。相對於載波的功率必須在這兩個頻率點間進行積分,然後按照公式六來加以計算。
其中L(f) 以功率密度比為單位,ΦSSB為單旁波帶整合相位雜訊rms,以度為單位。(當然,在頻譜分析儀中該公式會採總和而非積分的方式。)
以dBc為單位,整合的rms單旁波帶相位雜訊為:
兩個旁波帶的功率加在一起會變成2倍大:
現在,我們知道在公式五中的PSS/Pc單旁波帶功率比與ΦSSB計算值是相同的,因此:
公式九是在頻譜分析儀中進行的計算,指出rms相位偏差在整合相位雜訊上的量測結果,單位為度。根據rms相位偏差所做的一些簡單運算,對其他的應用來說會很有用。
抖動的單位為秒,可利用整合相位偏差與未調變載波在FC頻率下的一個時間週期的關聯性來進行計算。
圖三顯示使用X系列信號分析儀,在接近1 GHz的頻率下,對未調變載波的相位雜訊進行對數圖量測(log plot measurement)。該量測設定從偏離載波100 kHz到1 MHz的位置量測相位雜訊。標記1、2和3分別以dBcSSB、度和秒為單位來顯示相位雜訊。
標記4和5以分貝/倍頻(dB/octave)為單位,來顯示相位雜訊的斜度。標記6和7則以分貝/十倍頻(dB/decade)為單位,來顯示相位雜訊的斜度。
結語
大部分的新型頻譜分析儀,都會自動計算以上討論的所有公式中的結果。但知道這些公式是如何導出的,會有助於瞭解或計算這些結果,這一點是其他頻譜分析儀的相位雜訊量測無法提供的。有些量測還可以使用內建的頻帶功率標記來自動執行,以便為必須完成的工作開發特殊的量測。
(本文由Agilent安捷倫科技提供)