引線接合 (Wirebond) 被廣泛被使用於半導體元件上,做為晶片端點與外部引腳間的連接。使用在引線接合上的引線一般是由黃金所製造的,這是因為黃金具備抗氧化、高導電的特性,且相對容易與 IC 端點以及元件引腳接合。
然而,由於銅線有著較優異的電氣特性,以及相對較低的金屬間化合物增長及提升的力學穩定性等熱屬性,所以用銅線來取代金線的方式,也已經在逐漸發展中。
在像是電源管理 IC 這類有著高直流電流流通的元件上,大量的引線被使用來承載這些電流。這些額外的引線可以幫助改善直流壓降 (IR Drop) 的效能,以及降低因高電流流通產生的熱(焦耳加熱現象)所造成的引線熔斷或熔解的風險。很不幸的是,現在並沒有任何方法或分析方式,可以預估特定應用下所需使用的引線數量及尺寸。一般不是對於使用的引線數量估計太過悲觀,導致晶圓面積及成本的增加;要不然就是太樂觀,而造成信賴度風險上昇及元件故障。
這篇文章旨在討論不同尺寸及種類的引線,其預估直流電流處理能力之方法,所提供的準則將可協助產品設計工程師預估特定應用所需引線的最適化數量。
理論上電流承載能力之預估
典型的引線熔斷設計方程式是由 W.H. Preece 所發展出來的(於 1884 年,被稱為 Preece 方程式),僅應用於存在於自由大氣中的引線。
針對以安培為單位的熔斷電流,以及以英吋為單位的引線直徑,此方程式建立了兩者之間的關聯,方程式如下所示。
- i = 直流 (DC) 或 均方根值 (RMS) 電流
- k = 常數,該數值取決於引線的材料而定 (對黃金及銅而言, k = 10,244)
- D = 以英吋為單位的引線直徑
這個方程式的限制在於它僅應用於存在於自由大氣中的引線。而且,它也沒有將導線的長度納入考量。引線的電流承載能力是與長度相關的,而且是長度增加時,則預期承載能力會下降。
修正的 Preece 方程式
為了解決上述提到的限制,Preece 方程式被修正成使用較高的常數 k 值,來反映一般應用中的實際情況,也就是引線是被以環氧樹脂為基礎的壓模成型材料所包覆的。常數 k 值也反映了長度對於引線電流承載能力的影響效應。導線長度 ? 0.040 英吋時,包括黃金及銅的 k 值都是 30,000,而當導線長度 > 0.040 英吋時,則 k 值為 20,500。
以軍事規格 (MIL-M-38510J) 呈現的方程式,是以修正的 Preece 方程式為基礎。
表一列出針對兩種導線形式,分別以兩個版本的 Preece 方程式計算出來的電流承載能力。
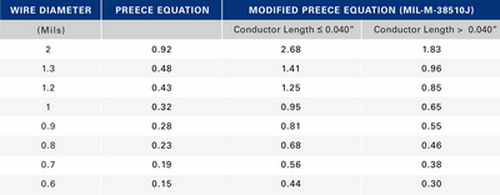
| 表一 : 以 Preece 方程式為基礎的電流承載能力 |
|
使用修正的 Preece 方程式依然存在一些限制:
- (1)電流承載能力數值顯示是與材料無關的。銅與黃金相比,其導熱性高出百分之二十,而導電性則高出百分之三十,所以就理論上而言,銅應該能夠比黃金處理較多的電流。
- (2)這個方程式並沒有推算出導線長度超過 0.040 英吋(大約 1 公厘的引線長度)之後的電流承載能力。大多數的應用上,引線長度是在2公厘到3公厘的範圍之間,有時還會超過。引線的電流承載能力會隨著導線長度的改變而有著很顯著的不同,而這個方程式則無法解釋這一個部分。
- 有鑑於上述的限制性,我們需要一個新的方法,這個方法必需以已知的幾何形狀及材料屬性,以及該典型應用所造成的限制為基礎。
在導線中的焦耳加熱
當電流流經一個電阻有限的非理想導線時,熱會被釋放出來,而這個將電能轉換成熱能的過程被稱為焦耳加熱或電阻加熱。被釋放出來的熱量是直接與流經導線中的電流平方值以及電阻值成正比。它的關係是:
對於被靜止的空氣所環繞的導線而言,所有產生的熱,都透過導線消散掉,而沒有熱從導線表面被帶走。這個系統會在以下情況達成穩定狀態:
所產生的熱透過導線而消散掉,是使用如下所顯示的一個簡單熱轉移傳導過程的方程式。
- k =引線的導熱係數
- A = 引線的截面積
- dT = 引線兩端的溫度差
- dx = 引線長度
重新安排上述方程式並予以簡化成,
- k=引線的導熱係數;對黃金而言,k = 310 W/mK,而對於銅而言,k=390W/mK
- ρ=引線的電阻係數;對黃金而言,ρ=2.44e-8 Ω-m,而對於銅而言,ρ=1.68e-8 Ω-m
- D=引線的直徑
- l=引線長度
- ΔT=引線兩端的溫度差;假設在最大的電流能力計算時為常數
再進一步簡化成:
根據以上的關係,假設一切保持不變,則銅應該能夠比黃金多處理百分之二十五的直流或是均方根值電流。
在大多數實際應用中,熱不僅是透過導線被帶走,也會從導線的表面透過環氧樹脂壓模成型材料,以放射狀方向被帶走。這種結合的現象是複雜的,而且無法以封閉型方程式來精確地分析。因此,有著熱電耦合物理解法 (thermal-electric coupled physics solver) 的有限元素模型軟體 (finite-element modeling software),就被用來分析不同的導線變數所造成的效應。
應用說明及模型的建立
一個典型的引線接合封裝結構,在晶片上會有一個焊墊,以引線與封裝的引腳相連接,引線的材質主要是黃金或是銅。圖一顯示一個典型的封裝構造。
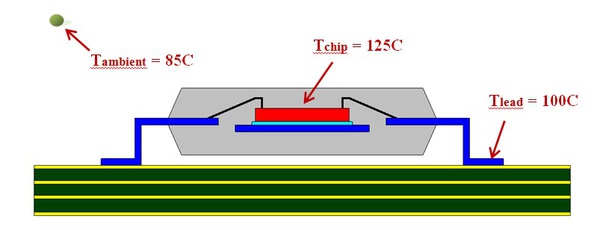
| 圖一 : 在印刷電路板上,有著相關溫度監測點的封裝 |
|
商業應用會限制最高的環境溫度不可超過攝氏70 度,而在工業應用上則是限制溫度不得超過攝氏85度。大多數的應用會註明最大的晶片接面溫度 (junction temperature) 是在攝氏 125 度,而有些應用則是註明此一溫度為攝氏 150 度。
為了預估引線在最壞情況下的電流承載能力,因此在這個模型內,我們假設工業環境溫度是設定在最高的晶片接面溫度 – 攝氏125度。我們將自然對流邊界條件(Natural convection boundary condition) 應用在封裝的表面,同時封裝引腳溫度為攝氏 100 度。
小量的電流流經引線,並不會改變在橫越引線跨距範圍內的溫度剖面,因此引線兩端依然維持在原始的相同溫度。當流經的電流逐漸增加時,則最熱的溫度將不再是處於晶片接面處,而是在引線跨距中間的某處。
模壓成型材料 (mold compound) 的玻璃過渡溫度(Tg) 是一種材料從硬的、且相對較脆的狀態,過渡到一個軟的、類似橡膠狀態時的溫度,其一般典型的溫度大約在攝氏 150 度。假如流經引線的電流,導致模壓成型材料超過它的Tg時,時間與溫度將會降低在這個接面上環氧樹脂材料的化學鍵。這不僅會導致模壓成型材料熱阻的增加,同時也會造成材料疏鬆性的增加,使其暴露在濕氣及其他離子性污染物侵入的狀態下。因此,我們假設引線的模壓成型材料的接面溫度為攝氏150度,此為計算引線電流承載能力時的最大溫度限制值。
以此做為標準來分析引線材料種類、引線長度及引線直徑所造成的效應,並將這些資料與理論上的預估值進行比較。
圖二顯示使用三種方式所得到有關 1 mm長黃金引線之電流承載能力的資料。使用有限元素模型 (FEM) 所得到的電流值,在一開始的時候與使用修正的 Preece 方程式所得到的結果大約在相同水準,但是隨著引線直徑的增加,則得到的結果開始不同。
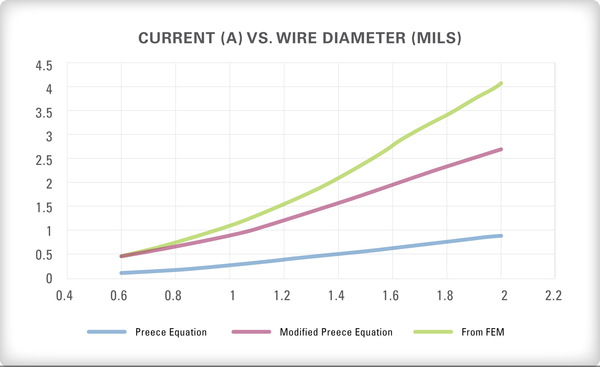
| 圖二 : 使用有限元素模型 (FEM) 與 Preece 方程式所得到 1 mm長的黃金引線之電流承載能力 |
|
圖三顯示使用有限元素模型 (FEM) 方法所得到 1 mm長的黃金引線與銅引線的電流承載能力。如預期的,銅引線承載較多電流的能力優於黃金引線。
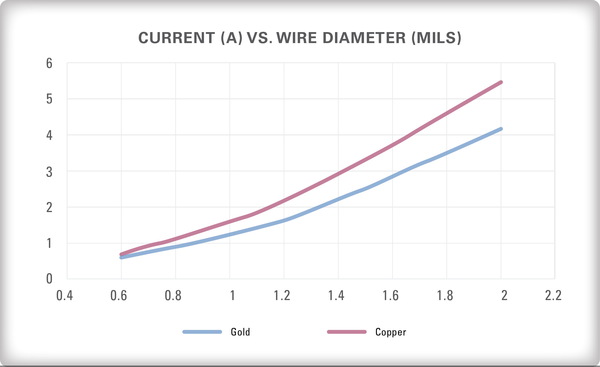
| 圖三 : 使用有限元素模型 (FEM) 方法所得到 1 mm長的黃金引線與銅引線的電流承載能力 |
|
圖四顯示使用有限元素模型(FEM) 方法所得到三種不同長度黃金引線的電流承載能力。如預期的,當長度增加時,引線的電流承載能力會降低。表二總結了不同引線組合的電流值(以安培為單位)。
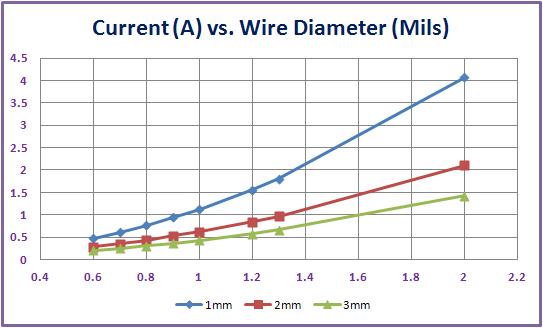
| 圖四 : 使用有限元素模型 (FEM) 方法所得到三種不同長度黃金引線的電流承載能力 |
|
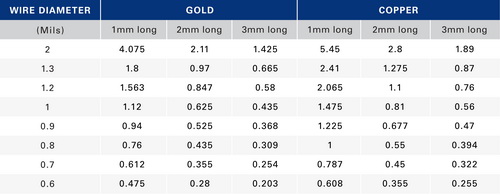
| 表二 : 不同引線組合的電流值(以安培為單位)摘要 |
|
總之,這篇文章闡明了在實際應用環境下,引線材料種類、引線長度及引線直徑對引線的電流承載能力所造成的效應。它也說明了由傳統方法所得到的電流承載預估值的限制性。
- (本文作者為Integrated Device Technology公司首席工程師)