五種最壞情況雜訊分析與設計法則
多數運算放大器資料表只會列出運算放大器雜訊的一般值,至於雜訊的溫度漂移資料則多半付之如闕。因此,電路板和系統級設計人員希望有方法能讓他們根據一般值估計雜訊的最大值及溫度漂移。雖然電晶體的某些基本雜訊關係能幫助估計這些資料,但想精確運用這些關係,就需要知道偏壓方式和電晶體種類等某些內部架構的細節;不過若能考慮最壞情況下的架構,就有可能以它為基礎得到涵蓋多數架構的某些一般性描述。本文首先整理出五個關於最壞情況雜訊分析與設計的基本經驗規律,然後詳細說明這些經驗規律背後的數學原理。
經驗法則1
寬頻電壓雜訊對半導體製程的改變相當遲鈍,這是因為運算放大器雜訊大都是運算放大器偏壓電流的函數。一般而言,偏壓電流並不會隨著元件有太大改變,但也有些設計的雜訊主要來自輸入靜電防護電阻(input ESD protection transistor)的熱雜訊。只要瞭解此點,就知道寬頻雜訊的變動不太可能超過一般值的10%;事實上,多數低雜訊元件的寬頻雜訊變異都少於10%。圖一就是例子。
但對雙極性製程而言,寬頻電流雜訊就比電壓雜訊敏感,這是因為電流雜訊與基極電流有關,而基極電流由電晶體的電流增益(β)決定。寬頻電流雜訊頻譜密度的變異在正常情況下不會超過30%。
《圖一 根據一般值估計室溫下的最大寬頻雜訊》 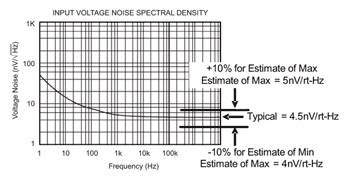 |
經驗法則2
運算放大器雜訊隨著溫度而增加。在許多偏壓機制裡(例如與絕對溫度成比例的PTAT架構),雜訊會隨著絕對溫度的平方根等比增加,因此雜訊在工業溫度操作範圍內的變化其實很小,例如25~125℃範圍可能只有15%。但也有些偏壓機制產生的雜訊與絕對溫度成正比,例如零溫度係數(Zero-TC)機制就是如此。在這種最壞情況下,雜訊在同樣溫度範圍的改變幅度可能高達33%。圖二就是這種情形。
《圖二 一般和最壞情況的雜訊溫度漂移》 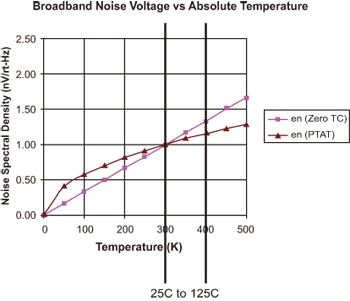 |
經驗法則3
1/f雜訊(閃爍雜訊)會受到製程很大影響,這是因為1/f雜訊與晶片製造過程會導致晶態結構瑕疵,所以只要半導體製程控制良好,1/f雜訊的強度就不會有太大變動。生產問題或製程變動都會大幅改變1/f雜訊,若元件資料表列出1/f雜訊的最大值,就表示製程受到監控或元件會在最後測試階段接受測量;若資料表未提供1/f雜訊的最大值,則可假設製程控制並未將1/f雜訊抑制最佳化,而且最壞情況下的雜訊變異幅度估計會達到原來三倍。詳情請參閱圖三。
《圖三 最壞情況下的1/f雜訊估計值》 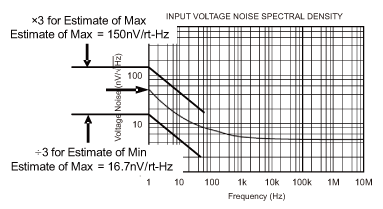 |
經驗法則4
電路板與系統級設計人員須瞭解靜態電流(Iq)與寬頻雜訊為負相關。嚴格來說,雜訊與運算放大器輸入差動級的偏壓有關。但因這項資訊通常不公開,可以假設靜態電流與差動級偏壓成正比。這個假設對低雜訊放大器最精確。
寬頻雜訊通常與靜態電流的平方根成反比,但此關係會隨著偏壓機制不同而改變。這個經驗法則應有助於電路板與系統級設計人員進一步瞭解靜態電流與雜訊之間的取捨。舉例來說,設計人員不應期望放大器同時擁有超低的靜態電流和低雜訊。靜態電流與雜訊的關係如圖四所示。
《圖四 靜態電流與寬頻雜訊的關係》 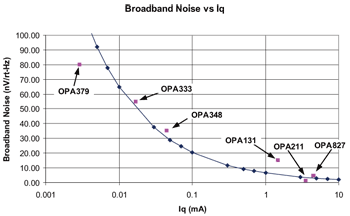 |
經驗法則5
FET運算放大器的電流雜訊本來就很小,這是因為FET電晶體與雙極性不同,FET的輸入閘極電流遠小於雙極性放大器的輸入基極電流。反過來說,在特定偏壓電流下 (亦即輸入級的集極或汲極電流),雙極性放大器的電壓雜訊通常較低。
雙極性電晶體雜訊的數學分析
圖五是雙極性電晶體雜訊模型的電路圖,圖六則為雙極性電晶體的基本雜訊關係 (公式一、二和三)。本文接著將計算這些公式,以便顯示這些經驗法則背後的基本關係。
《圖五 雙極性電晶體雜訊模型》 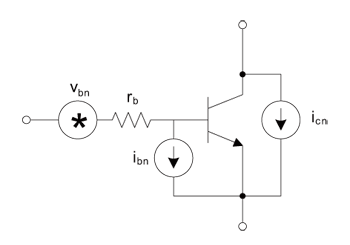 |
《圖六 雙極性電晶體雜訊的基本關係》  |
利用公式一進行分析
公式一代表雙極性電晶體基極的實體阻抗熱雜訊。在積體電路運算放大器裡,這個電阻通常來自差動輸入級基極所串聯的靜電保護電路(參考圖七),該雜訊有時會成為主要雜訊來源。對多數積體電路製程而言,此電阻的公差可假設為±20%。圖八顯示20%的輸入阻抗變異會造成10%的雜訊變異。
《圖七 運算放大器雜訊的熱雜訊分量》 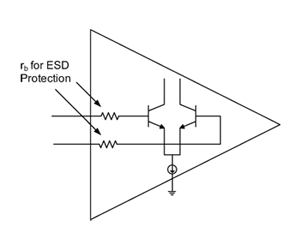 |
《圖八 熱雜訊公差》  |
利用公式二進行分析
公式二代表雙極性電晶體集極散粒雜訊(shot noise)的關係,不僅能把它轉換為電壓雜訊vcn以更深入瞭解這項關係(參考圖九),還能在知道輸入級偏壓機制的情形下進一步簡化該公式。運算放大器輸入級的偏壓機制可分為兩種,第一種機制會強迫集極電流與絕對溫度成正比(PTAT),這種PTAT偏壓機制的集極電流可表示為絕對溫度與某個常數的乘積。圖十是根據PTAT偏壓機制簡化得到的vcn公式,其重點是雜訊變成與溫度的平方根成正比,與集極電流(Ic)的平方根成反比。這個重要結果顯示為何低雜訊放大器的靜態電流總是很大,這也是經驗法則5的基礎。此結果還顯示運算放大器雜訊會隨著溫度而增加,這則是經驗法則2的依據。
《圖九 把電流雜訊轉換為電壓雜訊》  |
《圖十 PTAT偏壓機制下的集極雜訊電壓》  |
運算放大器的輸入級也能採用零溫度係數(Zero-TC)偏壓機制,此時集極偏壓電流不會隨著溫度而漂移。圖十一是根據零溫度係數偏壓機制簡化得到的vcn公式,其重點是雜訊變成直接與溫度成正比,並與集極電流的平方根成反比。零溫度係數架構比較容易受到溫度變化的影響,這是它不如PTAT機制的地方。注意在經驗法則2裡,這就是最壞情況下的雜訊溫度漂移。
《圖十一 零溫度係數偏壓機制下的集極雜訊電壓》  |
圖十和十一的結果可用來計算雜訊如何隨著集極電流而改變。基本上,這兩種偏壓機制的雜訊都與集極電流的平方根成反比。在積體電路運算放大器設計裡,差動輸入級經常是主要的雜訊來源,可惜這款放大器的資料表並未提供偏壓機制的相關資訊。為了獲得粗估值,可以假設集極電流的變化與靜態電流的變化成正比。由於輸入級偏壓電流的控制通常比靜態電流更容易,所以這項估計算是相當保守。圖十二為最壞情況下的雜訊估計值,注意此時靜態電流變異對雜訊幾乎沒有影響。在多數實際設計裡,這個變異不會超過10%。注意經驗法則1是以熱雜訊變異和散粒雜訊變異(集極電流變異)都不會超過10%的事實為基礎。
《圖十二 根據靜態電流 (Iq) 變異得到的最壞情況雜訊》  |
利用公式三進行分析
公式三描述雙極性電晶體基極的散粒雜訊和閃爍雜訊,這個雜訊源就像是運算放大器的電流雜訊,而且該電流雜訊還能轉換為電壓雜訊(參考圖十三)。至於PTAT和零溫度係數偏壓架構的分析,則不像集極電流散粒雜訊的情形那麼簡單,這是因為這兩種偏壓方式都是用來控制集極電流,基極電流並不會遵循這項關係。舉例來說,雙極性電晶體的電流增益會隨溫度改變,所以零溫度係數集極電流的元件將不會有零溫度係數基極電流。
公式三的散粒雜訊分量是寬頻電流雜訊的主要來源。注意該雜訊電流與基極電流的平方根成正比,這是寬頻電流雜訊比寬頻電壓雜訊更敏感的原因。基極電流的變異是由電晶體的電流增益所造成。
注意該散粒雜訊分量的形式與公式二相同,因此分析方法也完全一樣,只不過基極電流的溫度係數很難預測。因此為了簡單起見,不會把基極電流散粒雜訊的溫度資訊包含進來。
圖十三把閃爍雜訊分量轉換為電壓雜訊。注意閃爍雜訊會隨著溫度而增加,並隨著集極電流而減少。然而閃爍雜訊對製程改變很敏感,因此閃爍常數(K1)的變異可能成為該雜訊的主要影響因素。這與寬頻雜訊的情形並不同,因為寬頻雜訊的常數與製程無關。這是經驗法則3的基礎。
《圖十三 閃爍雜訊電壓關係》  |
FET雜訊背後的數學原理
圖十四為MOSFET和JFET電晶體雜訊模型的電路圖,圖十五則為FET電晶體的基本雜訊關係(公式四和五)。接下來將運算這些公式,證明該經驗法則同樣適用於FET電晶體。圖十六是以處於強反轉區(strong inversion)的FET為對象,計算它在PTAT和零溫度係數偏壓機制下的熱雜訊公式。強反轉區是FET的一種偏壓區,它會讓熱雜訊與汲極電流(Id)的四次方根成反比;此時隨著偏壓方式不同,熱雜訊會與絕對溫度的平方根或四次方根成正比。因此相較於雙極性放大器,處於強反轉區的FET放大器比較不會受到靜態電流或溫度改變的影響。
《圖十四 雙極性電晶體雜訊模型》 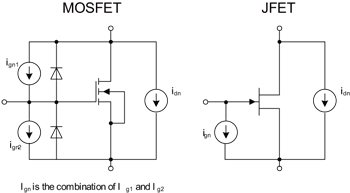 |
《圖十五 FET雜訊的基本關係》  |
《圖十六 FET處於強反轉區時的熱雜訊》  |
圖十七則是以處於弱反轉區(weak inversion)的FET為對象,計算它在PTAT和零溫度係數偏壓機制下的熱雜訊公式。弱反轉區是FET的一種偏壓區,它會使熱雜訊與汲極電流的平方根成反比;此時隨著偏壓方式不同,熱雜訊會與溫度或其平方根成正比。因此當FET放大器處於弱反轉區時,其熱雜訊與電流或溫度的關係就與雙極性偏壓放大器很像。
《圖十七 FET處於弱反轉區時的熱雜訊》  |
圖十八以處於強反轉區的FET為對象,計算它在PTAT和零溫度係數偏壓機制下的閃爍雜訊公式。注意a是介於0.5和2之間的常數,因此隨著a值不同,閃爍雜訊有可能正比於汲極電流或反比於汲極電流的某個次方。閃爍雜訊在零溫度係數的偏壓機制裡與溫度無關,在PTAT偏壓機制裡則與溫度的平方根成正比。
《圖十八 FET處於強反轉區時的閃爍雜訊》  |
圖十九以處於弱反轉區的FET為對象,計算它在PTAT和零溫度係數偏壓機制下的閃爍雜訊公式。注意a是介於0.5和2之間的常數,因此閃爍雜訊在所有情形下都反比於汲極電流的某個次方。閃爍雜訊在零溫度係數的偏壓機制裡與絕對溫度成正比,在PTAT偏壓機制裡則與a值有關。
《圖十九 FET處於弱反轉區時的閃爍雜訊》  |
結語
本文討論幾個經驗法則,它們能協助估計最壞情況雜訊和雜訊溫度漂移,並幫助電路板與系統級設計人員瞭解IC設計人員在低雜訊設計中所做的取捨。文中還詳細說明這些經驗法則背後的數學原理。本系列的第8篇文章將深入討論1/f雜訊和爆米花雜訊 (popcorn noise)。
---作者Art Kay為德州儀器資深應用工程師---