錯誤更正碼簡介
在現今使用的通訊系統中,錯誤更正碼一直扮演著舉足輕重的腳色,其主要作用在於更正經過傳輸媒介時所產生的錯誤。目前廣泛地應用於各式的有線通訊、無線通訊以及各式的儲存裝置中。從另一方面來說,使用更錯能力較好的錯誤更正碼可以容許資料傳送端以較小的功率傳送信號,而接收端依然能正確地解回信號,達到減少耗能的效果。
目前常見的錯誤更正碼包含里德所羅門碼(Reed-Solomon Codes)、渦輪碼(Turbo code)及低密度奇偶校驗碼(Low-density Parity-check Codes)等。其中的低密度奇偶校驗編碼(簡稱為LDPC)最早是由Robert Gallager博士在1962年於其博士論文中發表[1],並且已被證實具有極為優越的性能。然而當時的科技卻無法實現這種編碼系統,低密度奇偶校驗編碼也就逐漸被人們所遺忘。直至三十多年後,隨著科技的進步和超大型晶體電路的製程不斷的演進,要實現低密度奇偶校驗編碼系統已不再是不可能的任務;同時以往所使用的編碼系統已漸漸無法滿足人類對於資料傳輸正確率與日俱增的需求,低密度奇偶校驗編碼終於在1995年由MacKay與Neal兩位博士重新發現並加以研究,能夠將資料傳輸正確率推至趨近向農極限(Shannon limit)[2],如圖一所示。因此,低密度奇偶校驗編碼已廣受通訊標準制定者的興趣。
![《圖一 位元錯誤率(BER)與信噪比(SNR)的比較圖。[2]》](/art/2008/07/011138020460/P1.gif)
| 《圖一 位元錯誤率(BER)與信噪比(SNR)的比較圖。[2]》 |
|
低密度奇偶校驗碼簡介
低密度奇偶校驗編碼是定義在一個稀疏矩陣(sparse matrix)上,在矩陣之中大部分的元素為0,只有少數的元素為1。而一個(n,k)低密度奇偶校驗編碼所對應奇偶校驗矩陣的維度是(n-k)*n,如圖二是一個(16,8)低密度奇偶校驗編碼所對應的奇偶校驗矩陣。

| 《圖二 (16,8)低密度奇偶校驗編碼的奇偶校驗矩陣。》 |
|
在解碼上,可以把奇偶校驗矩陣轉換為二分圖(bipartite graph),如圖三為(16,8)低密度奇偶校驗編碼的二分圖。轉換方式是將奇偶校驗矩陣中的列和行分別對應成圖三的方形實心圖案和圓形空心圖案,其對應處理單元分別為檢查點單元(Check Node Unit;CNU)和變數點單元(Bit Node Unit;BNU)。再將元素為1所對應行列的處理單元,用直線相連。每條直線代表檢查點單元和變數點單元之間訊息的傳遞。在一般實際的應用上,低密度奇偶校驗矩陣的長度至少是數百甚至可達數萬之譜,因此矩陣中元素1的量也會很大,對應到實際的硬體架構時,也代表CNU和BNU之間的連線會非常複雜,同時也使得硬體所需面積增大。
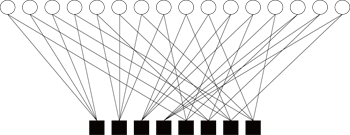
| 《圖三 (16,8)低密度奇偶校驗編碼的二分圖。》 |
|
在CNU和BNU這兩種運算單元中執行的運算有數種不同的演算法,目前較常使用的有和積演算法(Sum-product Algorithm;SPA)以及最小和演算法(Min-sum Algorithm;MSA)。前者的錯誤更正能力極佳,但是牽涉的運算相當複雜,對硬體上的實現較為不利;後者則可視作是SPA簡化後的版本,在表現上雖會略差一點,但是卻大大地降低了運算複雜度。為了彌補MSA在表現上的不足,近期也有相當多的論文專門探討如何增加些許額外的運算就能讓MSA的錯誤更正能力更接近SPA,此類的方式也稱作修正最小和演算法(Modified Min-sum Algorithm)。
在硬體的實現上大致可分為全平行式(Fully-parallel)和部分平行式(Partially-parallel)運算。全平行式的運算方式需要較多的運算單元,但是由於其平行展開的特性,所以特別適用於有高速度需求的通信系統;部分平行式的運算架構相對於前者則只需要較少的運算單元,但是缺點是速度也會比全平行式運算架構降低不少,適用於低傳輸低功率消耗要求的系統。
在眾多低密度奇偶校驗碼的矩陣設計方式中,為了兼顧錯誤更正能力和硬體實現上的複雜度,於是發展出了一種稱為準循環式(Quasi-cyclic)的矩陣結構。此種架構雖然會使得LDPC的錯誤更正能力變差一些,但是由於它具有局部性循環的效果,得使硬體設計的複雜度大大降低,目前如IEEE 802.11n和IEEE 802.16e皆採用此類結構。
低密度奇偶校驗解碼器實現之挑戰
在實現LDPC編解碼器的過程中,最大的困難有以下幾點:
解碼矩陣不易建立
依照最原始的理論來說,想要求得一個解碼效果好的矩陣只要讓矩陣中數值的位置隨機散佈即可,但是依這種方式建構出的矩陣由於不具規律,所以相當不利於實際LDPC解碼器的硬體實現;然而太有規律的矩陣則會損害其解碼的成效。因此如何在兩者間取得一個平衡也是一門重要的課題。
編碼器的硬體複雜度高
因為所謂的低密度矩陣指的是解碼端的矩陣,若直接由此倒推回編碼端的編碼矩陣通常不是一個低密度矩陣,而且也難以找到規律,間接造成編碼端的複雜度大大地提高。
硬體有效使用率低
由於LDPC解碼時是疊代地來回運算,所以並非所有的運算單元隨時都在運作,同時也造成解碼時間上的浪費。
多模式操作
現今的通信系統中幾乎都有多模式操作的特性,主要是為了配合不同的傳輸通道情形以及不同使用者的需求而設置。那麼在解碼端的設計上如果只是直接地做出數個LDPC解碼器將是十分缺乏效率的作法,只會浪費大量的硬體面積。
降低耗能
耗能的議題在行動通訊系統中特別重要,假設裝備同樣的電池,若是晶片耗能越低則該設備的使用時間就可越長。就一般的LDPC解碼方式而言,在解碼端需要經過多次疊代運算才能將正確的資訊解出,若能有效地減少此處的疊代運算次數,或是減少在運算時的大量記憶體耗能,必能達到低耗能的目的。
繞線(Routing)複雜度高
在硬體實作的最後一步就是如何佈置各單元間的繞線,由於LDPC的運算特性會使得繞線特別複雜,甚至常會有繞不出來的情況,所以如何將各個單元做適當的擺置以簡化繞線難度也是不可忽視的問題。
低密度奇偶校驗編解碼器之實現
以目前最熱門的兩個規格—IEEE 802.16e和IEEE 802.11n來說:前者是應用於移動中的車輛環境,後者則是適用於局部性的區域網路。其著眼點各有不同,應用於前者的LDPC編解碼器相當需要有低耗能的特性;用於後者則要求要有極高的解碼速率,其吞吐量(Throughput)的要求甚至是前者的數十倍。
以下以IEEE 802.16e(Mobile WiMAX)規格為範例,展示一個可提供19個模式之LDPC解碼晶片,這19個模式各有自己定義的原始訊息長度(information bits)、編碼後長度(codeword)。由於在訂定規格時就已經將LDPC解碼端的矩陣訂好,所以此處我們並不討論解碼矩陣的制定方式。我們在此提出一個簡單的解碼器架構設計:(1)以重新排列矩陣的方式減少解碼時間,(2)做出支援多模式之位址產生器,(3)採用了提前終結機制以減少運算耗能,(4)使用棋盤式的擺置方法放置記憶體以降低繞線複雜度。
解碼矩陣重新排列
由於LDPC解碼時是由兩種不同的運算單元疊代解碼,若照原本的作法每次都只會有一半的運算單元運作,而另一半的運算單元則處於閒置狀態,換句話說解碼端運算單元的硬體使用率只有50%,不啻是硬體的浪費,也間接地增加了解碼所需的時間。我們可以在完全不影響解碼效能的情況下做矩陣的重新排列,藉此達到兩種運算單元可以在部分時間同時運算的效果,增加硬體使用率也同時減少解碼所需的時間。最後可以將各時間的硬體平均使用率提高至75%,解碼時間也可以縮短為原本的67%,而所花費的成本僅是少許的控制電路。
多模式位址產生器
為了能同時支援Mobile WiMAX LDPC 19個模式,我們仔細觀察解碼端的低密度矩陣,在不同的操作模式下,各個運算單元和其所對應記憶體的存放位址會有所不同,最直接的方式當然是將各個運算單元與可能所需的記憶體以多工器(Multiplexer)相連,但是這樣的方式缺乏效率,而且為數眾多的多工器也會佔去不少的硬體面積。於是我們最後找出這19個模式互通的規律,做出適用於此規格的記憶體存取位址產生器,有效地達成同時支援19個模式的目標。
提前終結機制
最後解碼的錯誤多寡與否其實和信號通過傳輸介質後所得的信噪比(Signal-to-Noise Ratio;SNR)有很大的關係:若傳輸通道的雜訊越強,所得信噪比越低,不利於解碼;反之,若傳輸通道的雜訊越小,所得信噪比越高,有利於解碼。在信噪比越低的情況下,通常需要越多的疊代運算次數才能達到應有的效能;相反來說,在高信噪比的情況下可能只需要少數幾次的疊代運算就能將所有信號正確解出。
若能在僅損失些許的解碼效能前提下,達到提前結束不必要解碼運算的功能,將能大幅地減少解碼端的耗能。依此原則,有各式不同的機制被提出,有些機制較複雜但比較不會影響解碼效能,有些則強調其機制的簡易性。無論是何種機制,基本上都是在資源(硬體面積、耗能)和效能兩方面做取捨。
棋盤式擺放記憶體
在Mobile WMAX標準中所定義的LDPC解碼矩陣屬於準循環式矩陣,也就是在該大矩陣下的每一個小區塊中都有自己的局部循環性規律,在此設計中共有上百個記憶體。採取的是棋盤式的擺設方式,如圖四所示,如此排列的好處在於使運算單元至各個記憶體間不會形成過長的路徑,也同時減低繞線的複雜度。並能將不需要使用的記憶體關閉,達到節能的效果。
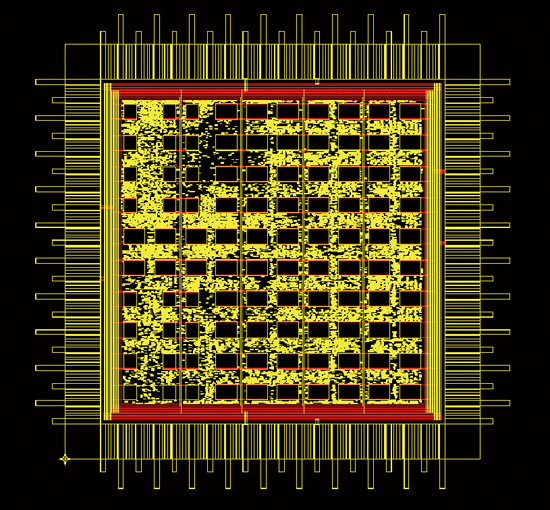
| 《圖四 晶片的佈線圖,其中的黑色方塊是記憶體所在位置。》 |
|
結論與未來展望
本文運用數個技巧實現了一個適用於Mobile WiMAX多模式低功率低密度奇偶校驗編解碼器,其硬體實作數據摘要和比較如表一所示。
低密度奇偶校驗碼在錯誤更正能力上的優良是無庸置疑的,目前已引起全世界學術界跟業界的注意,目前台大實作出了第一顆同時支援Mobile WiMAX多模式的LDPC晶片,也已經發表在2007 IEEE Symposium on VLSI Circuits(SOVC)會議上。但是仍然礙於實作時面積太大,尤其是其中大部分的空間都是用於繞線,致使要完全實際納入商品規格中仍有困難。未來或許可朝向如何解決繞線問題以及如何以合理的硬體達到高速的LDPC設計為目標繼續研究。
參考資料
[1] R. Gallager, “Low-Density Parity-Check Codes,” IRE Trans. Inf. Theory, vol. 7, pp. 21–28, Jan. 1962.
[2] D. J. C. MacKay, “Good Error-Correcting Codes based on Very Sparse Matrices,” IEEE Trans. Inf. Theory, vol. 45, no. 3, pp. 399–431, Jan. 1999.
[3] X.-Y. Hu, E. Eleftheriou, D.-M. Arnold, and A. Dholakia, “Efficient implementations of the sum-product algorithm for decoding LDPC codes,” in Proc. IEEE Globecom, vol 2, Nov. 2001, pp. 1036–1036.
[4] D. J. C. MacKay, “Good Error-Correcting Codes based on Very Sparse Matrices,” IEEE Trans. Inf. Theory, vol. 45, no. 3, pp. 399–431, Jan. 1999.
[5] D. J. C. MacKay, “Good Error-Correcting Codes based on Very Sparse Matrices,” IEEE Trans. Inf. Theory, vol. 45, no. 3, pp. 399–431, Jan. 1999.
[6] I. C. Park and S.H. Kang, “Scheduling algorithm for partially parallel architecture of LDPC decoder by matrix permutation," in Proc. IEEE ISCAS, May 2005, pp. 5778–5781.
[7] S. M. Kim and K. K. Parhi, “Overlapped decoding for a class of quasi-cyclic LDPC codes,” in Proc. IEEE SiPS, Aug. 2004, pp. 113–117.
[8] Blanksby, A.J. and Howland, C.J., “A 690-mW 1-Gb/s 1024-b, rate-1/2 low-density parity-check code decoder, ” IEEE Journal of Solid-State Circuits, Volume 37, Issue 3, March 2002, pp. 404 - 412
[9] Darabiha, A., Carusone, A.C., and Kschischang, F.R., “Multi-Gbit/sec low density parity check decoders with reduced interconnect complexity, ” ISCAS 2005, Vol. 5, May 2005, pp.5194 – 5197
[10] Mansour, M.M. and Shanbhag, N.R., “A 640-Mb/s 2048-bit programmable LDPC decoder chip, ”IEEE Journal of Solid-State Circuits, Volume 41, Issue 3, March 2006, pp. 684 – 698