頻譜密度 (spectral density) 是雜訊的重要特性。電壓雜訊頻譜密度是每平方根Hz的均方根 (RMS) 雜訊電壓 (通常寫成nV/√Hz),功率頻譜密度則是W/Hz。上一篇文章曾介紹過,電阻的熱雜訊可由方程式2.1計算,該方程式可重新寫為頻譜密度的形式。熱雜訊的重要特性是頻譜密度相當平坦 (亦即能量均勻分佈在所有頻率),因此熱雜訊有時被稱為寬頻雜訊 (broadband noise),運算放大器也有寬頻雜訊。本文將寬頻雜訊定義為頻譜密度很平坦的雜訊。
除了寬頻雜訊外,運算放大器通常還包含頻譜密度並不平坦的低頻雜訊區域,這個雜訊稱為1/f雜訊、閃爍雜訊 (flicker noise) 或低頻雜訊。1/f雜訊的功率頻譜通常會以1/f的速率下降,這表示電壓頻譜是以1/f(1/2)的速率下降。然而在實際上,1/f函數的指數可能會略有出入。(圖一)是包括1/f區域和寬頻區域在內的典型運算放大器頻譜。注意該頻譜密度圖中還包括電流雜訊 (表示為fA/√Hz)。
注意1/f雜訊也是常態分佈,因此第一篇文章介紹的數學仍然適用。(圖二)是1/f雜訊在時域的波形,注意該圖的X軸是以秒為單位 – 這種隨著時間緩慢改變的現象正是1/f雜訊的典型特性。
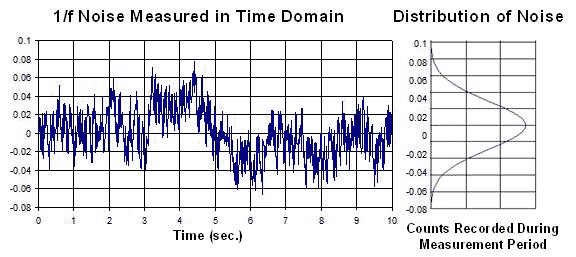
| 《圖二 以時域和統計方式顯示的1/f雜訊》 - BigPic:575x256 |
|
運算放大器雜訊的標準模型如(圖三)所示。在運算放大器輸入端,有兩個不相關的電流雜訊源和一個電壓雜訊源。電壓雜訊源可視為時變輸入偏移電壓分量,電流雜訊源可視為時變偏壓電流分量。
運算放大器雜訊分析技巧
運算放大器雜訊分析技巧的目標,是根據元件資料表的資訊,計算運算放大器電路的峰對峰輸出雜訊。接著本文將以適用於大部分簡單運算放大器電路的公式,來解釋這項技巧。對於較複雜的電路,這些公式對所預期的雜訊輸出也能有粗略概念。為複雜電路發展出更精確公式是可能的,但其數學部份往往過於複雜。處理複雜電路最好採用三個步驟的做法:首先利用公式取得粗略估計,其次利用Spice產生較精確估計,最後透過測量驗證結果。
以德州儀器 (TI) 的OPA277非反相放大器做為簡單的電路範例 (圖四)。為了求得峰對峰輸出雜訊,必須把運算放大器電流雜訊、運算放大器電壓雜訊和電阻熱雜訊都列入考慮。我們除了將利用資料表的頻譜密度曲線得到雜訊源的數值,還會考慮電路的增益與頻寬。
首先,要將雜訊頻譜密度曲線轉換成雜訊源數值,必須透過一些微積分計算。簡單來說,函數積分可以得到函數曲線下方的面積。(圖五)顯示常數函數的積分其實等於高度乘以寬度 (亦即矩形的面積)。這個簡單關係可以將頻譜密度曲線轉換成雜訊源數值。
想要求得總雜訊,一般人認為要對電壓頻譜密度曲線積分。但實際上得對功率頻譜密度曲線積分,而這條曲線其實就是電壓或電流頻譜密度曲線的平方 (P=V2/R和P=I2R)。(圖六)顯示以電壓頻譜密度曲線積分後所得到的奇怪單位。(圖七)顯示如何對功率頻譜密度進行積分,然後取平方根將結果轉換回電壓,這能得到正確的單位。
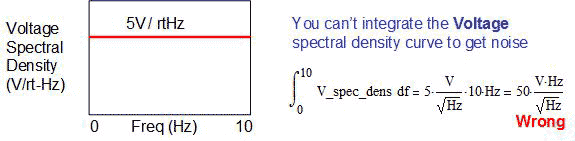
| 《圖六 不正確的雜訊計算方式》 - BigPic:574x141 |
|
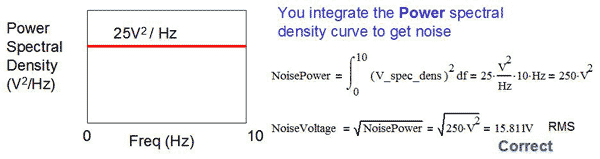
| 《圖七 正確的雜訊計算方式》 - BigPic:599x158 |
|
對功率頻譜密度曲線積分求得電壓或電流頻譜後,就能知道運算放大器模型的雜訊源均方根振幅 (圖三)。然而頻譜密度曲線會包含1/f雜訊區,及帶有低通濾波器的寬頻雜訊區 (圖八),計算這兩個部份的總雜訊必須用到前面以微積分導出的公式,然後利用第一篇文章介紹的非相關雜訊源和方根值 (Root Sum Square,RSS) 加法,把這兩個結果加在一起。
首先對帶有一個低通濾波器的寬頻雜訊區進行積分。在理想情形下,這條曲線的低通濾波器部份是一條垂直線,稱為磚牆濾波器 (brick wall filter)。磚牆濾波器下的矩形面積很容易計算 (寬度 × 高度),可惜在實際應用裡無法做出完美的磚牆濾波器。儘管如此,仍有一組常數,可將實際的濾波器頻寬轉換成等效的磚牆濾波器頻寬,以便計算雜訊。(圖九)是理論上的磚牆濾波器與一階、二階和三階濾波器的比較。
(公式二)可用來轉換實際濾波器或等效的磚牆濾波器。(表一)列出了不同濾波器階數的磚牆轉換因子 (Kn)。舉例來說,只要將一階濾波器頻寬乘上1.57,就能轉換成磚牆濾波器頻寬,調整後的頻寬有時又稱為雜訊頻寬。隨著濾波器階數增加,轉換因子會逐漸趨近於1;換言之,階數越高的濾波器就越像是磚牆濾波器。
透過實際濾波器轉換為等效的磚牆濾波器公式,可以簡化頻譜積分的計算。請記住,功率積分就是電壓頻譜的平方,所以積分結束後再取平方根即可轉換回電壓。(公式三)就是以這種方式導出 (參考附錄2.1)。因此,利用(公式二)和(公式三),再配合元件資料表的資訊,便可求得寬頻雜訊強度。
(表一) 磚牆修正因子
濾波器極點數目 |
Kn
交流雜訊頻寬比 |
1 |
1.57 |
2 |
1.22 |
3 |
1.16 |
4 |
1.13 |
5 |
1.12 |
回想一下,本文的目標是根據(圖三)決定雜訊源Vn的振幅,而這個雜訊源同時包含寬頻與1/f雜訊。透過(公式二)和(公式三)已可計算出寬頻雜訊分量,現在還需要計算1/f分量,而方法是在雜訊頻譜密度圖裡對1/f區域的功率頻譜積分。此區域的圖形如(圖十)所示,積分結果可從(公式四)和(公式五)求得。(公式四)將1/f區域的任何雜訊正規化為1Hz位置的雜訊。有時從圖裡可直接讀取這個數字,有時使用這個方程式比較方便。(公式五)利用正規化雜訊、上方雜訊頻寬 (upper noise bandwidth) 和下方雜訊頻寬 (lower noise bandwidth) 計算1/f雜訊,完整的推導過程請參考附錄2.2
由於1/f函數在頻率等於零的位置沒有定義 (亦即1/0沒有定義),我們分析1/f雜訊時必須選擇一個低頻截止點。事實上,往回積分到0Hz時,雜訊值在理論上會是無限大。不過可將很低的頻率視為很長的時間。舉例來說,0.1Hz相當於10秒,0.001Hz相當於1000秒,至於極低頻率的對應時間則可長達數年 (例如10nHz等於3年)。積分的頻率區間越寬,得到的雜訊就越大。但請記住,極低頻雜訊的測量必須涵蓋一段很長時間。這些現象將在後面的文章深入討論,現在只要知道0.1Hz常被做為1/f計算的下方截止頻率。
寬頻和1/f雜訊的振幅都已經得到,現在必須利用第一篇文章介紹的不相關雜訊源公式,將這些雜訊源相加。參考本系列第一篇文章的(公式八)。
工程師在考慮這種積分技巧時,經常會認為1/f雜訊和寬頻雜訊應在兩個不同的區域進行積分;換言之,他們相信由於1/f雜訊會與「1/f區域」外的寬頻雜訊相加,使得直接在這個區域中相加雜訊會得到錯誤結果。其實1/f區域和寬頻區域一樣都涵蓋所有頻率。要記住,雜訊頻譜是繪在對數圖上,所以1/f區域降到寬頻曲線下方後就幾乎不再有任何影響。只有在相交點附近的區域 (通常稱為1/f角頻率) 才需將這兩條曲線合併考慮。您會發現在這個區域裡,這兩條曲線會以上述數學模型所描述的方式組合在一起。(圖十一)顯示兩個區域實際上如何重疊,另外它還顯示了一部份的相對振幅。
到目前為止,要將雜訊頻譜密度曲線轉換成雜訊源,其所需的全部方程式皆已發展出來。這些方程式雖是針對電壓雜訊所導出,但同樣的技巧也適用於電流。在本系列的下一篇文章中,將利用這些方程式處理運算放大器電路的雜訊分析。
結論和預告
本文介紹了運算放大器雜訊模型,雜訊頻譜密度曲線,以及部份基本的雜訊方程式。本系列的第3篇文章將以實際電路為例介紹雜訊計算。
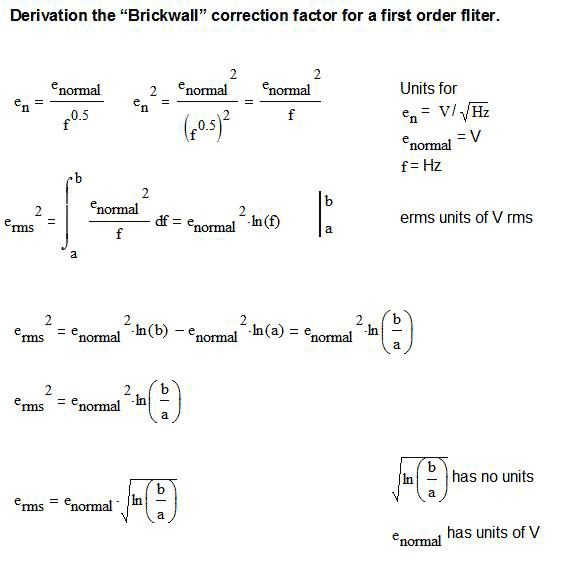
| 《圖十三 附錄二 一階濾波器的「磚牆」修正因子推導過程。》 - BigPic:574x569 |
|