低密度奇偶校驗編碼簡介

由於低密度奇偶校驗編碼（low-density parity-check code）提供極高的編碼增益，已經納入成為新世代通訊標準的一部份。相較於渦輪碼（Turbo code），在妥善的設計下，低密度奇偶校驗編碼解碼器具有較低的計算複雜度。完全平行解碼的實現方式，必須面對極高的繞線複雜度與大量硬體計算資源需求等問題。雖然完全序列處理可以用最少的硬體完成解碼器的設計，但是這樣的解碼器的解碼速度也是最慢的。部分平行解碼的硬體架構可以提供不同應用領域一個複雜度與傳輸速率平衡點。

二階段的訊息傳遞（two-phase messaging passing）解碼過程中，在第一階段的每一個訊息都會與通一列的訊息經過一個列運算（row operation），並產生第二階段所需要的訊息。訊息經過第一階段的處理後，每一個在同一行的訊息將經過一個行運算（column operation）。在每一個訊息完成二階段的運算後，稱為完成一次疊代解碼(decoding iteration)。當沒有使用任何排程演算法時，二階段訊息傳遞解碼必須先完成所有的列運算後才可以執行行運算。在此種情況下造成負責計算列運算或是行運算的硬體相互等待，導致硬體使用效率（hardware utilization efficiency）低落。

在設計者在設計低密度奇偶校驗編碼時，同時都會考量編碼設計對於解碼器的影響。許多的設計者採用類迴旋低密度奇偶校驗編碼（Quasi-cyclic low-density parity-check code），利用此種編碼結構化（structured）的特性降低解碼器設計的複雜度。相對於亂數產生的編碼方式（Random code），傳統的類迴旋奇偶校驗編碼在編碼長度大時，編碼增益（coding gain）低落。

階層式類迴旋低密度奇偶校驗編碼

由於類迴旋低密度機偶校驗編碼的奇偶校驗矩陣（parity-check matrix）是由多個循環矩陣（circulant matrix）組成，因此此種非常適合用於硬體實現。階層式類迴旋奇偶校驗編碼的建構方式，則是先建立一個 m x n 的二元核心矩陣（core matrix）。將此核心矩陣中的1與0分別以大小為 q1 x q1循環矩陣與q1 x q1零矩陣（zero matrix）取代，在這樣的矩陣展開（matrix expansion）後，可產生一個如同傳統類迴旋奇偶校驗編碼的奇偶校驗矩陣。對此已展開的矩陣再以q2 x q2 的循環矩陣與q2 x q2零矩陣取代1與0。在經過兩次的矩陣擴展後，可以得到一個二階層的階層式類迴旋（two-level hierarchical quasi-cyclic）奇偶校驗編碼的奇偶校驗矩陣。

《圖一　二階層階層式類迴旋奇偶校驗編碼校驗矩陣》

二階層的階層式類迴旋奇偶校驗編碼除了與傳統類迴旋奇偶校驗編碼一樣易於硬體實現。在電腦模擬的結果顯示（圖二），可以發現二階層的類迴旋奇偶校驗編碼提供接近隨機編碼的編碼增益外，也沒有如同類迴旋奇偶校驗編碼在高信號雜訊比（signal to noise ratio）區的error floor現象。二階層的階層式類迴旋奇偶校驗編碼可以套用任何可使用在類迴旋奇偶校驗編碼上的排程演算法。Jump-Reset排程演算法[1]（圖三）是一個可以使用在類迴旋奇偶校驗編碼的排程演算法，此排程演算法的效率優於Y. Chen [2] 所提出的排程演算法。Jump-Reset排程演算法亦符合Y. Dai [3] 所提出的最佳演算法的約束（constraint），且利用在二階層的階層式類迴旋奇偶校驗編碼時可以將硬體使用效率從50%提升至100%。

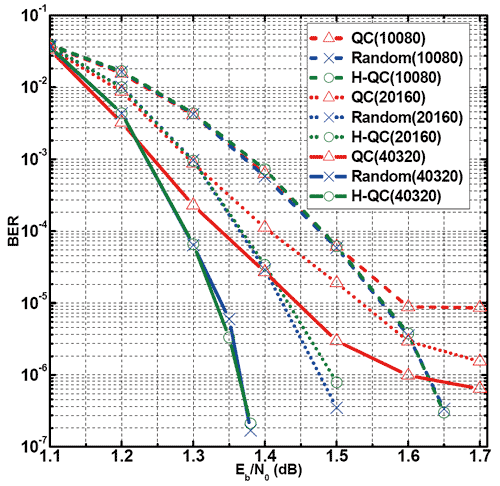
《圖二　類迴旋編碼、隨機碼與二階層的類迴旋編碼模擬結果》

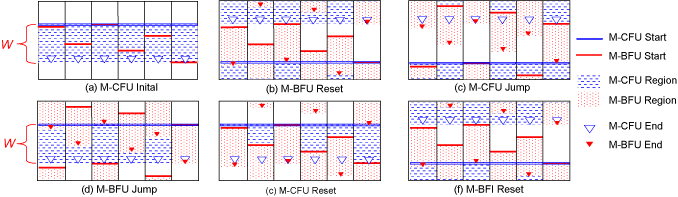
《圖三　Jump-Reset排程演算法》 - BigPic:678x197

二階層的階層式類迴旋奇偶校驗編碼提供了兩個參數q1, q2 ，其中q1提供編碼長度的調整（即編碼增益）。在相同的編碼率（code rate）下，編碼長度較長的編碼可以提供較好的編碼增益（相對的，硬體複雜度與硬體資源需求也會增加）。此外，由於解碼器硬體實現上，在一個時脈週期完成q2個訊息計算。因此q2則是提供解碼平行度的調整，使得解碼器架構可以適用不同性質的應用。

實驗結果

為了提供高硬體使用效率，除了排程演算法的使用外，記憶體也必須要能夠支援列運算硬體與行運算硬體同時存取（concurrent access）。(表一)整理了一個二階層的階層式類迴旋奇偶校驗編碼解碼器硬體實現的成果。此解碼器已經實現了Jump-Reset排程演算法的技術但是尚未使用了記憶體交錯（memory interleaving），目前傳輸速率已可以達到298.10Mbps。為了實現高硬體使用效率，未來的硬體實現套用記憶體交錯可以在增加低於10%的邏輯單元提升50%的硬體使用效率外亦方便於工作時脈的提升，達到780Mbps以上的傳輸速率。

（圖四）比較傳統類迴旋奇偶校驗編碼與二階層的階層式類迴旋奇偶校驗編碼之硬體實現的編碼和軟體實現的編碼增益損失。類迴旋奇偶校驗編碼解碼器在編碼增益的部分優於傳統的類迴旋編碼，且硬體實現於位元錯誤率（bit error rate）10-5，僅因為有限的精準度而損失0.05dB以下。

《圖四　軟體實現與硬體實現的編碼增益比較》

結論

二階層的類迴旋奇偶校驗編碼搭配Jump-Rest排程演算法與記憶體交錯，可以提升硬體使用效率從50%至100%。此外，亦可以搭配合適硬體架構並藉由調整q1、q2參數廣泛的使用於不同的應用領域。

（顧孟愷先生為美國加州大學洛杉磯分校電機工程博士，現任台灣大學資訊工程研究所教授。

簡義興先生為台灣大學資訊工程研究所博士生。）

參考文獻

[1] Yi-Hsing Chien, Mong-Kai Ku, "A High Throughput H-QC LDPC Decoder," accepted by IEEE International Symposium on Circuits and Systems 2007 (ISCAS 2007)

[2] Y. Chen and K. K. Parhi, “Overlapped message passing for quasi-cyclic low-density parity check codes,” IEEE Trans. Circuits and Syst. I, vol. 51, pp. 1106–1113, Jun. 2004.

[3] Y. Dai and Z. Yan, “Optimal overlapped message passing decoding for quasi-cyclic low-density parity-check codes,” IEEE Global Telecommunications Conf. (GLOBECOM), vol. 4, pp. 2395–2399, Dec. 2005.