小數週期延遲濾波器是一種可用於內插離散訊號(DISCRETE-TIME SAMPLES)的裝置,而其內插的位置由一非整數的延遲參數D來決定。小數週期延遲濾波器可應用在非常多與信號處理相關的領域,如語言處理、音響儀器模型或數位接收機中的時脈補償電路。
實現小數週期延遲濾波器的架構主要可歸納為兩類:分別是有限脈衝響應(FIR)濾波器和無限脈衝響應(IIR)濾波器[1]。以前者為架構,最著名的是Farrow內插器。當輸入訊號能量集中在較低的頻段時,此內插器即可達到足夠的精確度並擁有低階數和低硬體複雜度的優點。然而,當輸入訊號能量散布至較高的頻段時,則會產生相當嚴重的失真及振幅上的衰減[2]。
若以後者為架構,可以Thiran濾波器為代表。此小數週期延遲濾波器透過其係數鏡射對稱性的設計,保證全頻段的量值響應(magnitude response)均具有單一相同(unity)增益。而此濾波器一樣是透過一個小數週期延遲參數d來控制。參考文獻[3][4]對此濾波器提出了電路設計,根據d,利用即時電路運算的方法來產生濾波器的所有係數。如此一來,當所需的濾波器的階數很高時,便會產生相當長的關鍵路徑延遲(critical path)和相當大的硬體使用量。
在本篇文章中,我們從Thiran濾波器的基礎出發,提出數種改良式的硬體架構,以避免上述提及的缺點。除此之外,本文還提出陰影濾波器(shadow filter)的概念,用來解決當控制非整數週期延遲濾波器的隨時變係數d產生溢位(overflow)時,所可能造成的電路不穩定(unstable)情形。
小數週期延遲全頻段通過濾波器之架構
Thiran非整數週期延遲全頻段通過濾波器
利用濾波器係數鏡射對稱性的設計,當一個N階的無限脈衝響應濾波器具有(公式一)的轉換函數(transfer function)時,不論係數ak的值為何,此濾波器即具有全通的特性。意即此濾波器在不同的輸入信號頻率下,其量值響應(magnitude response)均具有單一相同(unity)的增益,如(公式二)所示。
因此,當全通的特性已確定後,我們只需把重心移回至係數ak的設計上,也就是著重在相位響應(phase response)的部份,以達到小數週期延遲的功能。
Thiran小數週期延遲全通濾波器是以在零頻率點有最大平坦的群體延遲(maximally-flat group delay)來做設計上的限制條件。如此一來,Thiran濾波器從零頻率點到某一特定的頻率點(根據使用者的設計需求而定)均有平坦的群體延遲(線性的相位響應)。根據文獻[1],Thiran濾波器的係數公式為濾波器階數N和非整數週期延遲參數d的函數,如下(公式三)。
其中(d)k 是從d、(d+1)到(d+k-1)共k項的連乘積;且d的合理範圍為-0.5到0.5。此濾波器的輸出除了原有欲得到的小數週期延遲d以外,由於其無限脈衝響應的電路特性,還會具有N個時脈週期(clock)的延遲,故總延遲為(N+d)個時脈週期。
(表一) 關鍵路徑延遲比較
Type |
Critical path |
Real-time [4] |
( M+1 ) Tm + {M+1+  } Ta } Ta |
Table-lookup |
Tm + 5Ta |
Farrow內插器和Thiran濾波器的比較
為了要比較有限脈衝響應濾波器和無限脈衝響應濾波器兩者間的效能,我們選取2階4-tap的Farrow內插器[2]來和Thiran濾波器比較。(圖一)為理想Farrow內插器在頻域上的量值響應及其相對應的錯誤量。由圖一可知,在較高頻段上,Farrow內插器會使輸入信號的能量嚴重衰減,進而影響整個系統的效能。而Thiran濾波器則可完全免除掉這樣的缺點:由公式一、公式二兩式可知,即便濾波器係數經過定點數化(quantize)的處理,Thiran濾波器在全頻段的量值響應上,均確保了單一相同的增益。
在完成兩者頻域上的效能比較後,改以輸入真實訊號至Farrow內插器和Thiran濾波器,以比較兩輸出波形在時域上的效能差異,此時兩電路的非整數週期延遲係數d均設為-0.5。如(圖二),當輸入訊號為加成性白色高斯雜訊(AWGN)時,相較於Farrow內插器而言,Thiran濾波器因具有單一相同增益的特性,使其輸出保留了較多輸入訊號的高頻部份。如(圖三),當輸入訊號的能量是集中在較低的頻段上時(band-limited),則Farrow內插器和Thiran濾波器的表現差異較不顯著,但在輸入訊號變動較快的一些轉折處,仍可發現Thiran濾波器的輸出較能跟上輸入波形的變化,效能明顯較優。
總而言之,在時域效能的評比上,同樣以達成非整數週期延遲為目的,Thiran濾波器相較於Farrow內插器而言,更能忠實反應輸入訊號在高頻部份的細微變化。
傳統Thiran濾波器之架構
為了實現Thiran濾波器的演算法,傳統的作法是將(公式三)濾波器係數ak 的公式解拆成兩個多項式的相乘:其中一個多項式和d無關;另一個則是以d為冪次的泰勒展開式[4]。其A(z)的轉換函數如下(公式四)。
由公式三,濾波器的係數ak之分母具有控制小數週期延遲的參數d,當此濾波器要操作在即時係數更新的系統時,會造成硬體實現上的困難,而公式四的近似方法解決了這樣的問題,但也付出了下述代價:如多項式乘積的近似造成精準度的喪失,且大量的乘加器的使用產生更長的關鍵路徑延遲,和更大的硬體使用量。在假設文獻[4]中的M、N和I均相等的情況下,關鍵路徑延遲為(N+1)個乘法器和2N個加法器,並正比於濾波器階數N;而其硬體複雜度則是和階數N的平方成正比。
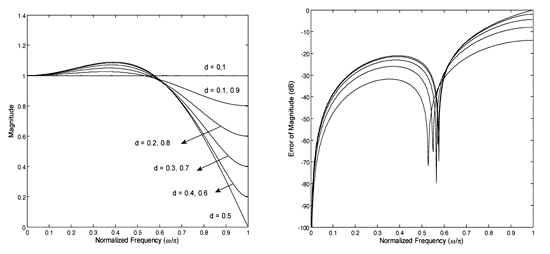
| 《圖一 理想2階4-tap Farrow內插器的量值響應(左圖)及其錯誤量(右圖)》 |
|
改良式的THIRAN濾波器架構
採用查表法來取得濾波器係數
在傳統的Thiran濾波器架構中,為了即時更新濾波器係數ak,造成相當長的關鍵路徑延遲。若採用查表法,以隨時變小數週期延遲參數d來做為查表的位址,則可避免此一缺點並同時保留即時更新係數ak的能力。在實施縮減延遲的電路技巧(retiming technique) 後,並將對稱係數的乘法器重覆使用,改良式的5階Thiran濾波器架構如圖四。如此一來,關鍵路徑延遲將固定為一個乘法器和五個加法器,而和濾波器的階數N無關。
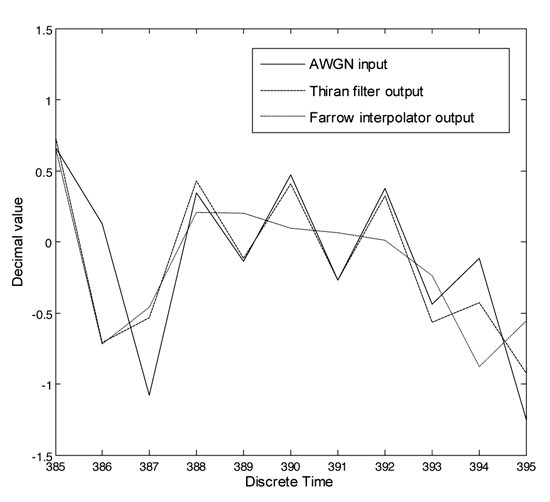
| 《圖二 時域上之輸入輸出波形模擬(輸入訊號為加成性白色高斯雜訊)》 |
|
採用線性近似法和兩階層查表法
Thiran濾波器的係數ak和小數週期延遲參數d具有一近似線性的關係,(圖五)是以5階Thiran濾波器為例所畫的圖。因此,若想進一步減低查表硬體的大小,我們可以先利用移位加法(shift-and-add)電路,根據d,來粗估濾波器係數ak的值。如此一來,查表內容只需存放理論值和近似粗估值間細微的差值即可,使得所需的查表硬體大幅縮小。
另一個可將查表大小再進一步縮小的方法是把存放上述細微差值的一個查表拆成兩層的查表。第一層的查表使用小數週期延遲參數d的前幾個位元(MSBs)做為查表的位址,而表內容儲存的是一個係數理論值減去線性近似值的粗調值。換句話說,若d前幾個做為第一層查表位址的位元均相同時,不論d剩下後幾個位元(LSBs)的值為何,都是對應到相同的粗調值。而第二層的查表則是使用d全部的位元來做為查表的位址,儲存的內容為係數理論值減去線性近似粗估和第一層查表粗估的值後,所剩下相當微小的差值。
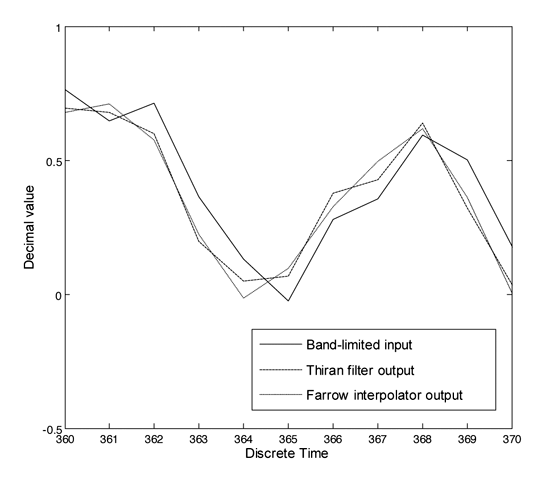
| 《圖三 時域上之輸入輸出波形模擬(輸入訊號的能量集中在較低頻段)》 |
|
設計實例
在此,我們舉5階Thiran濾波器來做為設計上的實例。我們給定其濾波器輸入和輸出、及小數週期延遲參數d的精確度均為10個位元。經過定點數的模擬後,濾波器的係數ak需要12個位元的精確度。由圖五,a1在量值上的變化遠較a2 到 a5為大,故以相同的精確位為基準, a2 到 a5需要的位元數遠較a1為少。故5階Thiran濾波器的係數組(a1, a2, a3, a4, a5)所需的定點數長度依序為(12, 11, 9, 7, 3)個位元。在使用單一查表的方法下,總查表的大小為1024*(12+11+9+7+3) = 43008 個位元。
若採用兩層的查表來進一步縮減表大小,則第一階層的查表需要d的前6個位元做為查表的位址;在達到和前述相同精確度的前提下,第一及第二層查表分別儲存係數組ak的粗調及微調值,其所需的定點數長度分別為(12, 11, 9, 7, 3)和(6, 5, 3, 2, 1)個位元。而此兩階層查表所需要的總位元數減少到20096個位元。
若同時採用線性近似及兩層查表的方法,則查表的部份只需儲存係數理論值和線性近似粗調值的差值部份。一樣以和前述相同精確度為前提,第一層的查表需要d的前7個位元做為查表的位址;而第一及第二層查表所需的定點數長度分別減少為(9, 9, 8, 5, 3)和(3, 3, 2, 1, 1)個位元。 如此一來,此兩層查表所需要的總位元數將進一步減少至14592個位元。此外,同時採用線性近似及兩層查表的方法不僅減小了查表硬體的使用量,亦能保有使用查表法後,所擁有固定關鍵路徑延遲的特性。其整體架構圖如(圖六)。
(表二) 硬體複雜度比較
Type |
Real-time
u pdate [4] |
One table |
Two
tables |
Linear
approxi.
& t wo tables |
Combinational area ( μ m 2 ) |
193709.09 |
156548.81 |
53638.41 |
45415.41 |
Noncombinational area ( μ m 2 ) |
21734.64 |
11675.64 |
11675.64 |
11675.64 |
Total cell area
( μ m 2 ) |
215447.61 |
168229.35 |
65313.86 |
57091.00 |
硬體比較
在本篇論文中,總共提及有四種Thiran小數週期延遲全通濾波器的設計:第一種為傳統透過兩個多項式相乘來取得係數的架構[4];而剩下的三種分別為使用一個查表、兩層查表、和同時採用線性近似及兩層查表的改良式架構。
(表三) 功率消耗比較
Type |
Real-time
u pdate[4] |
One table |
Two tables |
Linear
approxi.
& t wo tables |
Total d ynamic p ower ( μ W ) |
1254.40 |
776.60 |
510.04 |
530.67 |
Cell l eakage p ower ( nW ) |
984.03 |
800.42 |
311.91 |
245.67 |
Total p ower ( μ W ) |
1255.38 |
777.40 |
510.35 |
530.91 |
關鍵路徑延遲比較
和傳統Thiran濾波器架構相較,改良式架構利用查表的方法,所產生的最大改進為大幅減少關鍵路徑的延遲,並固定其關鍵路徑延遲的長度。而傳統做法為了達到係數的即時更新,其關鍵路徑的延遲將線性正比於濾波器階數N及參數M。(表一)為傳統架構和改良式查表架構之關鍵路徑延遲的整理比較。
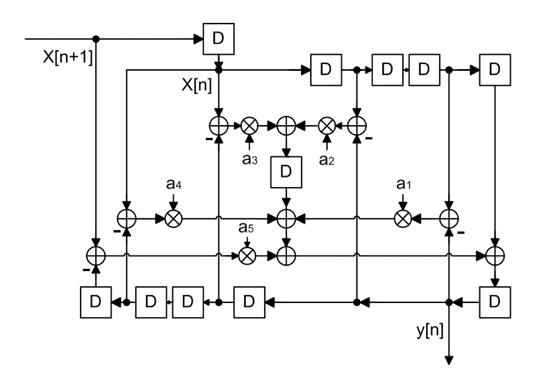
| 《圖四 5階Thiran非整數週期延遲全頻段通過濾波器硬體架構圖》 |
|
硬體面積和消耗功率比較
除了時間延遲上的效能改善外,改良式的架構亦可降低硬體面積和消耗功率。為了確保上述四種架構在硬體比較時的公平性,其濾波器的輸入和輸出及小數週期延遲參數d均給定為10位元的定點數長度;除此之外,查表內容的定點數長度均以達到最佳效能為選擇考量,如第四章第3小節所述。
在合成上述四種不同的濾波器架構時,採用軟體為設計編譯器(Design Compiler),並給定10MHz的系統時脈(clock)和典型的模擬環境假設(typical condition),而設計資料庫(design library)是採用聯電0.18μm的製程。由於相鄰d值的查表內容具有很高的相似性,因此,上述使用到查表法的架構均是使用組合式邏輯電路(combinational logic circuits)來實現;若採用暫存器檔案(register file)來實現查表,則硬體面積反較使用組合式邏輯電路為大。(表二)為四種架構在硬體面積上的比較表,在同樣達到係數即時更新的條件下,同時採用線性近似和兩層查表的改良式架構的電路面積僅為傳統架構的26.5%。
除此之外,由於查表法避免了傳統架構所需的大量乘法器,故可大幅縮減電路的消耗功率。由(表三)的功率消耗比較表可知,改良式架構相較於傳統架構而言,最多可減少59.4%的功率消耗。然而,加入線性近似法的改良式架構,需要移位加法(shift-and-add)的運算,所需的動態消耗功率會略較僅使用兩階層查表的架構為大。因此,是否加入線性近似的技巧於兩層的查表架構中,需要考量面積和功率間的取捨問題(trade-off)。
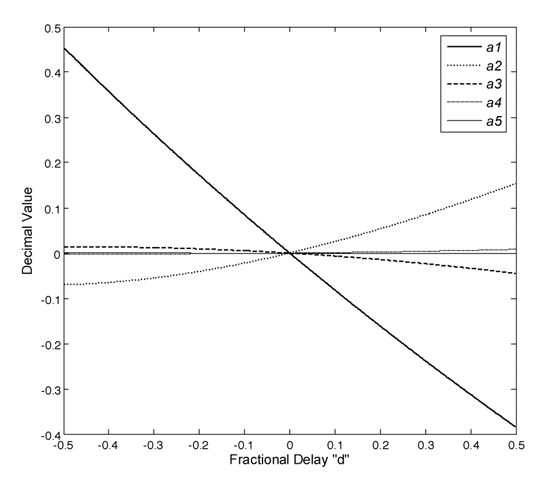
| 《圖五 5階Thiran非整數週期延遲全頻段通過濾波器之係數ak對d作圖》 |
|
取樣時脈漂移的補償電路
輸入緩衝暫存器(input buffer register)
Thiran濾波器使用可調整之小數週期延遲參數d來調控輸出和輸入訊號間小數部份的延遲;此外,為確保Thiran濾波器的穩定性(stability),d的範圍應落在-0.5至0.5之間。若d是落在此區間內的某個定值,則此時濾波器可正確無誤地運作。然而,當應用小數週期延遲濾波器於取樣時脈漂移的補償電路時,其d值通常為累加器的輸出,故溢位現象會不斷發生。當d值累加超過0.5時,即產生正溢位(overflow);累加至小於-0.5時,即產生負溢位(underflow)。解決溢位問題最簡單而基本的方法是加入一個輸入緩衝暫存器,即所謂的移位暫存器(shift register),如(圖七)所示。
假設此時小數週期延遲濾波器的輸入為x[n],當正溢位發生時,則濾波器的輸入應更新為x[n+1]。這個過程等同於將圖七的「窗戶(window)」向左移動一個移位暫存器的長度。若發生負溢位時,則此「窗戶」應向右移動一個移位暫存器的長度。
加入移位暫存器是有效解決溢位問題的方法,但要付出相當大的D flip-flop硬體是其最主要的缺點。若使用雙埠的靜態隨機存取記憶體(dual-port SRAM),並利用記憶位置對應(memory mapping)的方法:一方面將輸入訊號不斷地依序存入記憶體中,另一方面使用一個額外的暫存器來儲存讀取記憶體之位址,當溢位的情形發生,便修改暫存器內代表記憶體位址的值,以控制此時要輸入濾波器的訊號。這樣的做法可節省相當多的循序邏輯電路(sequential logic circuits)。而此取樣時脈漂移的補償電路所能忍受最大的溢位次數是根據輸入緩衝暫存器的長度或記憶體的大小而定。
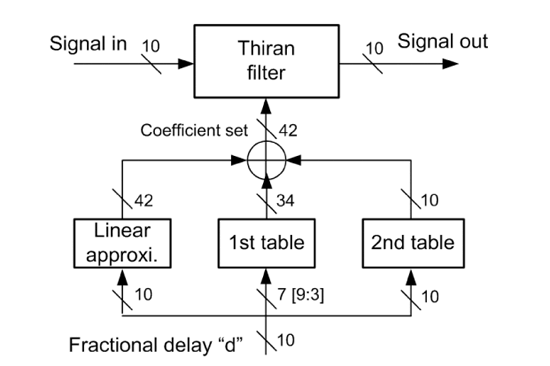
| 《圖六 利用線性近似及兩階層查表來取得濾波器係數ak》 |
|
陰影濾波器(shadow filter)
然而,單純考量輸入緩衝的設計並不能完全解決溢位時所發生的所有問題。當溢位產生後,由於瞬間d值的不連續,造成濾波器的係數會產生劇烈變化,見圖五,而儲存在濾波器內部的暫存器值也會隨之大幅改變。由於Thiran濾波器是一種無限脈衝響應濾波器的架構,這樣的改變會造成瞬間輸出的劇烈變動,並造成電路不穩定(unstable)的情形。
有鑑於此,當溢位發生後,直接將濾波器係數的值更新,而不考量內部暫存器的穩定,不是一個理想的作法。為了確保無限脈衝響應濾波器的穩定,我們加入了陰影濾波器的概念,主要是由一個固定d值參數的Thrian濾波器所構成(根據發生溢位的種類來決定d值為0.5或-0.5)。當溢位發生時,陰影濾波器內部暫存器的值將會立即地複製到可調式(主要的)Thiran濾波器內部的暫存器中,並同時更新濾波器係數ak的值。如此一來,將成功避免掉Thiran濾波器輸出波形可能產生的不連續情形。
取樣時脈漂移補償電路之硬體架構
取樣時脈漂移的補償電路如圖八所示。若此電路的取樣時脈漂移值為固定,則會造成非整數週期延遲濾波器的隨時變係數d每隔一段時間,即產生一次溢位。當圖八中的累加器產生正(負)溢位時,比較器會產生1個位元的控制訊號來告知陰影濾波器,將其內部暫存器的值複製到可調式Thiran濾波器的內部暫存器中。
而在下一個時脈發生時,(圖八)中的虛線區塊(window)會左(右)移一個暫存器的長度。除此之外,取樣時脈漂移值的最前一個位元(MSB)將會決定那一組係數(d為0.5時的係數或d為-0.5時的係數)會成為陰影濾波器的係數ak;並決定那一個移位暫存器的位置(x[n+1]或x[n-1])會成為陰影濾波器的輸入。透過這些額外電路所形成的保護機制,將可完全避免因溢位而可能造成濾波器輸出不連續的情形。
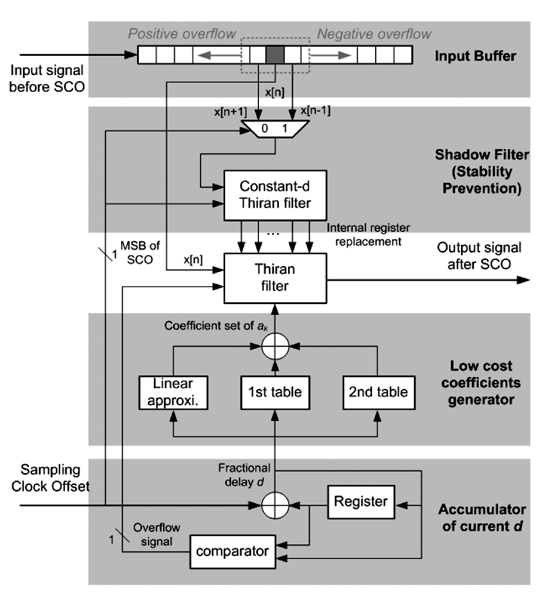
| 《圖八 整合改良式Thiran非整數週期延遲全頻段通過濾波器至取樣時脈漂移的補償電路》 |
|
結語
本論文提出了低硬體複雜度的改良式Thiran小數週期延遲全通濾波器設計。藉由查表法來取得係數ak,並使用縮減延遲的電路技巧後,將可大幅縮減並得到一個和濾波器階數N無關的固定關鍵路徑延遲。除此之外,同時使用線性近似和兩層查表的方法來即時得到濾波器係數ak,可再進一步減低硬體面積和消耗功率。總而言之,和傳統的Thiran濾波器相較,改良式的電路架構不僅保有濾波器係數即時更新的特性,也相當顯著地增進硬體的使用效率。
此外,本論文還提出陰影濾波器的概念,可完全避免小數週期延遲參數d產生溢位時,所可能產生的輸出錯誤和不穩定情形。將此概念整合至改良式的Thiran濾波器,本論文提出了新式取樣時脈漂移的補償電路。
---作者王拓評為台大電子所碩士班研究生、闕志達教授為台大電子所所長;本文作者感謝國科會研究計畫的補助,計畫編號為NSC95-2219-E-002-020---
<參考資料:
[1] T.I. Laakso, V. Valimaki, M. Karjalainen, U.K. Laine, “Splitting the unit delay,” IEEE Signal Processing Mag., vol. 13, pp. 30-60, Jan. 1996.
[2] L. Erup, F. M. Gardner and R. A. Harris, “Interpolation in digital modems II. Implementation and performance,” IEEE Tran. on Communications, vol. 41, pp. 998-1008, Jun. 1993.
[3] Makundi M., Valimaki V., Laakso T.I., “Closed-form design of tunable fractional-delay allpass filter structures,” in Proc. IEEE Int. Symp. Circuit and System (ISCAS 2001), vol. 4, pp. 434-437, May 6-9, 2001.
[4] Ji-Suk Park, Byeong-Kuk Kim, Jin-Gyun Chung, K. K. Parhi, “High-speed tunable fractional-delay allpass filter structure,” in Proc. IEEE Int. Symp. Circuit and System (ISCAS 2003), vol. 4, pp. IV-165- IV-168,?May 25-28, 2003.>