儘管感應馬達在過去數十年來逐漸被採用磁場導向控制( Field-Oriented Control;,FOC)技術的馬達所取代,但目前仍有數量眾多的感應馬達用於各種場合,因為它們仍是未來幾年內全球大規模節省能源消耗的絕佳目標。設備製造商只要採用磁場導向控制技術,就能讓應用系統改用較小的馬達。
磁場導向控制
磁場導向控制技術的運算量遠超過傳統純量技術,這是馬達控制設計工程師改用該技術時首先要考慮的設計衝擊。雖然磁場導向控制演算法的運算需求已超過傳統微控制器能力範圍,然DSP應付它們卻綽綽有餘。
DSP能大幅提高感應馬達的效率,使其從微控制器馬達常見的40%%增加至90%%。這種智慧型馬達還能改善功率因數,不但對電力公司是重大利多,也能讓設計工程師安心使用額定馬力較小的馬達,不必像現在一樣為了彌補低效率而採用超過實際所需的馬達。
不久之前,DSP的直接控制能力仍不如微控制器,磁場導向控制技術也因此無法被廣泛採用。但廠商近幾年已開始為DSP增加許多週邊功能,同時調整其架構以支援磁場導向控制演算法的特定需求,這些措施讓DSP效能變得更強大。
今日的馬達控制最佳化DSP不但整合所有必要週邊,還能在幾微秒內執行運算量龐大的控制演算法,以幫助製造商降低設備成本和耗電量。
感測器需求
磁場導向控制又稱為轉速或轉矩控制型交流馬達的向量控制技術,它是提高馬達動態效能的較好方法,現正迅速獲得市場廣泛接受。
第一代向量控制馬達是利用高精準度的轉速感測器以發揮最大效能,但轉速感測器會增加成本,可靠性也不理想。為了解決這些問題,業者開始發展和測試無感測器技術。
但在實際應用裡,傳統無感測器技術的效能卻不盡理想,主要問題在於馬達定子阻抗等參數會出現改變,這類參數變異會對低速或極低速運轉的馬達效率造成極大影響。這種現象在無感測器馬達上尤其嚴重,已成為無感測器控制技術廣泛應用的障礙。
工程取捨
設計工程師面臨兩難局面:高精準度感測器雖能提供精確量測結果,在惡劣環境裡卻不夠可靠;另一方面,低成本感測器則需要更複雜的運算處理。
工業應用對於馬達有著不同於一般的要求,除了低成本外,它們還必須能在惡劣環境下可靠工作。設計人員若想解決這個問題,就要採用更強大的參數估測技術以及具備訊號處理能力的運算引擎,例如新型的DSP元件。
採用強大參數估測技術以及低成本和低解析度轉速感測器的向量控制機制可在實際環境裡提供高效能,為了補償轉子時間常數變動所導致的滑差頻率(slip frequency)誤差,廠商還發展出一套校正程序。時間常數值的不確定性屬於一階問題,它會造成向量控制系統的調整失準,這套方法則能自行確定轉子的時間常數值,因此在導入設計時不必知道馬達的精確參數值。
磁場導向控制的基本原理
三相馬達通常會順著定子以三分之一或更小間隔的方式安排其線圈,我們因此只要利用相位相差1/3週期的三組電壓驅動這些線圈就能產生轉動磁場,(圖一)是它們的簡單示意圖。
感應電動機的轉子是由一組封閉線路組成,其中以鼠籠式轉子(squirrel cage rotor)的應用最廣泛,它會用很厚的金屬環將轉子導電棒短路。每當定子磁場掃過轉子時就會感應產生另一組磁場,這個磁場會與定子磁場交互作用產生(圖二)所示的馬達輸出轉矩,其強度是正比於轉子和定子磁通向量的外積,這表示在特定的電動機結構下,所產生的轉矩是由兩個磁場向量的強度以及它們之間的夾角決定。
對設計工程師來說,前述分析最重要的結論在於,若想有效產生轉矩,感應電動機的向量控制機制就必須能夠估測轉子磁通向量的正確角位置。
參數變異對磁場導向控制的影響
傳統的順向饋送式磁場導向系統會將負責控制磁通量和轉矩的兩組電流i*ds和i*qs視為輸入命令,再根據轉子時間常數T*r的輸入參考值和輸入電流值來計算滑差頻率ω*slip,並以它做為系統的輸入命令。
參數異動所導致的系統失調及其對於磁通量和轉矩的影響可由(公式一) 表示。當感應馬達處於穩定運轉狀態時,其輸出轉矩等於:
只要馬達受到磁場導向控制,滑差計算器(slip calculator)又設定正確的增益值,滑差頻率即可由(公式二)計算如下:
將公式二代入公式一即可得到轉矩和轉矩命令的線性關係式,但若馬達和模型參數不吻合,滑差頻率增益的計算結果就會出現錯誤。因此我們可在方程式公式二中引入一個稱為滑差頻率增益的純量值(α)來代表這種不吻合現象,此時公式二可表示為(公式三):
從公式一和公式三可發現,除非馬達和模型參數完全吻合(α=1),否則公式一 的非線性項就無法消去,這表示系統無法在最佳狀態下工作,其動態效能也將大幅下降。
自我調校程序
在特定的轉矩和轉速下,定子電流最小就表示每安培電流的轉矩最大。我們雖然能夠根據傳統方程式公式計算出多大的滑差頻率才能讓單位定子電流產生最大轉矩,但此頻率仍可能因為參數變異而出現誤差。
(圖三)是我們建議的控制系統,它與傳統控制系統很類似,最大區別在於它增加一個調校方塊(tuning block),負責調整磁場導向控制方塊圖中的滑差頻率增益值。調校方塊的最主要功能是找出正確的轉子時間常數。
把公式三 (3) 代入轉矩關係式中 (1),再將結果正規化即可得到一組非常有用的特徵轉矩曲線:
正規化轉矩TN是我們根據iqs/ids=1.0時的磁場導向轉矩所計算出的單位轉矩,這些特徵轉矩如(圖四)所示。
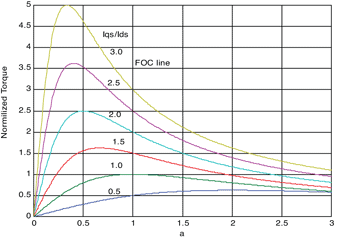
| 《圖四 正規化磁場導向特徵轉矩與滑差頻率增益誤差的關係圖:正規化磁場導向特徵轉矩與滑差頻率增益誤差的關係圖》 |
|
(圖四)將正規化轉矩TN表示成增益誤差α的函數,其中α=1的垂直線代表馬達處於磁場導向控制狀態,注意在這條直線上的轉矩值是的iqs/ids的線性函數。
圖四顯示除非ids等於iqs,否則向量控制技術就無法讓單位定子電流產生最大轉矩;反過來說,只要將特定轉矩和轉速下的定子電流減至最小,就能讓單位電流產生最大的轉矩。
在圖三建議的控制系統中,調校方塊負責調整向量控制方塊圖裡的滑差頻率增益,這項功能的關鍵在於找出轉子時間常數,同時確保其精確度符合要求。
調校程序開始後,速度控制器會暫停工作,改由調校方塊控制馬達轉速,它會根據ids和iqs調整電流大小使轉速保持不變,同時讓d和q電流振幅相等。此步驟產生的轉矩是由滑差頻率增益的變動值所控制。
接下來是以線性方式調整滑差頻率,使得ids和iqs在最大允許範圍內改變,然後記錄調整過程中出現的iqs(=ids) 最小值和當時的滑差頻率增益。
前述兩個步驟都會控制轉速保持不變,第二個步驟得到的滑差頻率則是調校後結果。取得滑差頻率增益的調校值後,需我們將調校方塊與控制系統的連線切斷,再把原來的轉速控制器接回控制迴路。接通迴路前應先調整轉速控制器輸出以確保電流保持不變,這能避免控制系統產生任何突然動作。
除了調整滑差頻率增益外,只要馬達處於穩定運轉狀態,這套程序就能用來將單位定子電流產生的轉矩調整為最大值;為避免電流飽和而導致過熱等問題,調整時應確保ids不超過額定範圍。
輸出轉矩在調整過程中必須保持不變。為了在穩態負載下提供固定輸出轉矩,這套演算法會在馬達處於低轉速時將轉速調整成其參考值;若馬達處於高轉速狀態,則會計算輸出轉矩。但在轉換狀態過程中或低速運轉負載出現變動時,轉矩也要跟著改變以穩定轉速,此時調校程序就會失效。
為了偵測馬達低速運轉時的任何負載變動並避免執行自我調校程序,系統只要發現計算所得的輸出轉矩改變超過5%就會送出暫停訊號給調校方塊,使它暫停調校動作直到下一個調校週期開始為止。輸出轉矩可由下列(公式六)計算: